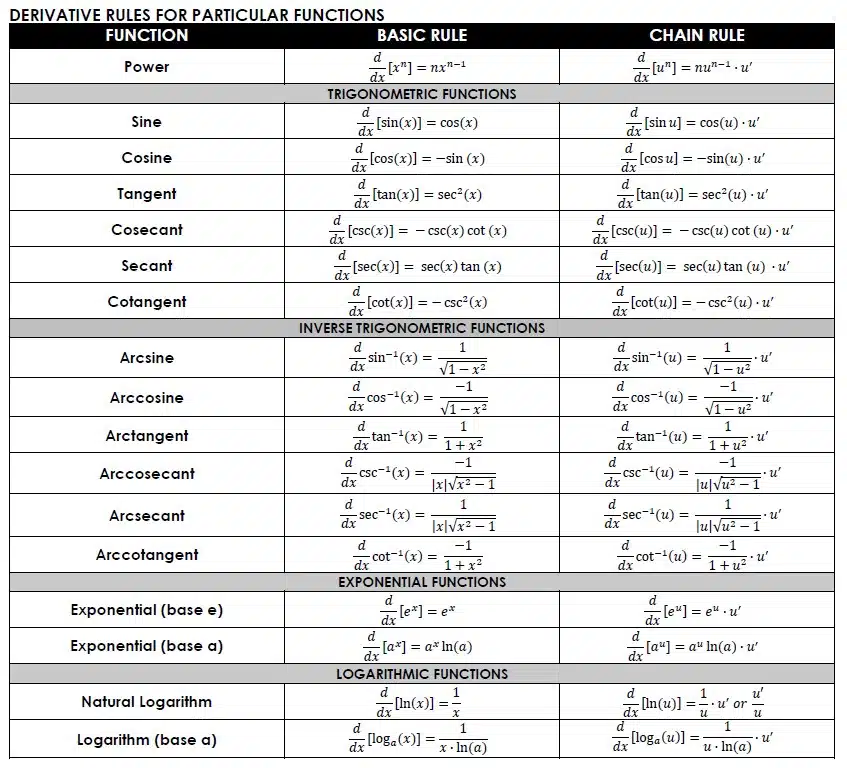
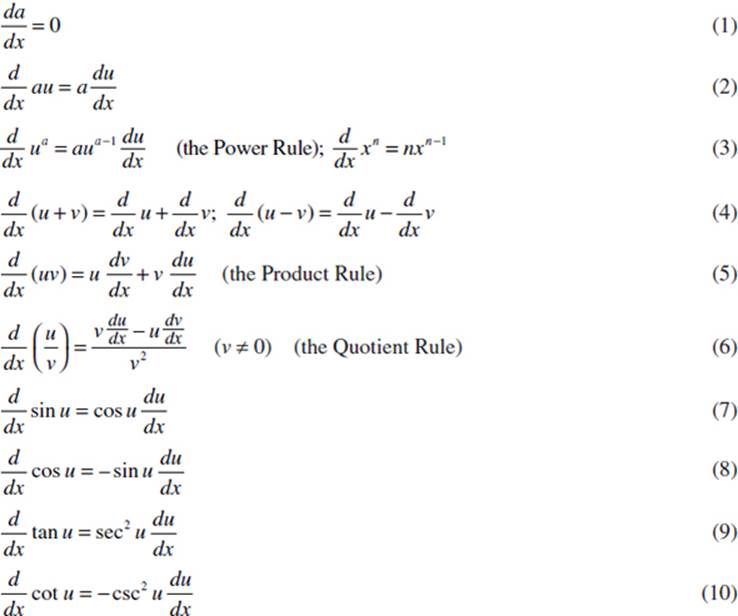Formula Of Differentiation Pdf - ππ(π₯π₯) Β± ππ(π₯π₯) β² = ππβ²(π₯π₯) Β± ππβ²(π₯π₯) 2. General rules of differentiation 1. The derivative of a constant is equal to zero. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. D dx (xn) = nxnβ1 z xn dx = 1 n+1 xn+1. ( m β n ) ! N β 1 1 n β 1 ! ( n β 1 ) ! Basic diο¬erentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize.
Basic diο¬erentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. ππ(π₯π₯) Β± ππ(π₯π₯) β² = ππβ²(π₯π₯) Β± ππβ²(π₯π₯) 2. N β 1 1 n β 1 ! The derivative of a constant is equal to zero. General rules of differentiation 1. D dx (xn) = nxnβ1 z xn dx = 1 n+1 xn+1. ( m β n ) ! ( n β 1 ) !
The derivative of a constant is equal to zero. ( m β n ) ! ππ(π₯π₯) Β± ππ(π₯π₯) β² = ππβ²(π₯π₯) Β± ππβ²(π₯π₯) 2. Basic diο¬erentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. N β 1 1 n β 1 ! D dx (xn) = nxnβ1 z xn dx = 1 n+1 xn+1. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. ( n β 1 ) ! General rules of differentiation 1.
Differentiation formulas for class 12 PDF Class 12 easy
( m β n ) ! N β 1 1 n β 1 ! D dx (xn) = nxnβ1 z xn dx = 1 n+1 xn+1. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. General rules of differentiation 1.
SOLUTION Differentiation all formula 12th class Studypool
( n β 1 ) ! D dx (xn) = nxnβ1 z xn dx = 1 n+1 xn+1. The derivative of a constant is equal to zero. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. ( m β n ) !
Free Printable Derivatives Formula Chart (PDF) Math = Love
N β 1 1 n β 1 ! If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. General rules of differentiation 1. ππ(π₯π₯) Β± ππ(π₯π₯) β² = ππβ²(π₯π₯) Β± ππβ²(π₯π₯) 2. The derivative of a constant is equal to zero.
Formidable Differentiation Formula Class 11 Physics 2nd Puc All Formulas
N β 1 1 n β 1 ! If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. ππ(π₯π₯) Β± ππ(π₯π₯) β² = ππβ²(π₯π₯) Β± ππβ²(π₯π₯) 2. Basic diο¬erentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. D dx (xn) = nxnβ1 z xn dx = 1 n+1 xn+1.
Differentiation formulas for class 12 PDF Class 12 easy
( m β n ) ! Basic diο¬erentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. D dx (xn) = nxnβ1 z xn dx = 1 n+1 xn+1. The derivative of a constant is equal to zero. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary.
Formula of Differentiation by chain rule With solved example
N β 1 1 n β 1 ! ππ(π₯π₯) Β± ππ(π₯π₯) β² = ππβ²(π₯π₯) Β± ππβ²(π₯π₯) 2. General rules of differentiation 1. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. Basic diο¬erentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize.
Differentiation Formula Limits at Jane blog
D dx (xn) = nxnβ1 z xn dx = 1 n+1 xn+1. Basic diο¬erentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. General rules of differentiation 1. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. N β 1 1 n β 1 !
Differentiation Formula for Trigonometric Functions
ππ(π₯π₯) Β± ππ(π₯π₯) β² = ππβ²(π₯π₯) Β± ππβ²(π₯π₯) 2. N β 1 1 n β 1 ! Basic diο¬erentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. ( m β n ) !
Basic Differential calculus, Math formulas, Differentiation formulas
The derivative of a constant is equal to zero. If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. ππ(π₯π₯) Β± ππ(π₯π₯) β² = ππβ²(π₯π₯) Β± ππβ²(π₯π₯) 2. N β 1 1 n β 1 ! ( m β n ) !
Image
( m β n ) ! If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. D dx (xn) = nxnβ1 z xn dx = 1 n+1 xn+1. The derivative of a constant is equal to zero. General rules of differentiation 1.
N β 1 1 N β 1 !
( n β 1 ) ! General rules of differentiation 1. Basic diο¬erentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. ππ(π₯π₯) Β± ππ(π₯π₯) β² = ππβ²(π₯π₯) Β± ππβ²(π₯π₯) 2.
D Dx (Xn) = Nxnβ1 Z Xn Dx = 1 N+1 Xn+1.
( m β n ) ! If y = c, = (c) = 0 dx d dx dy where βcβ is any arbitrary. The derivative of a constant is equal to zero.