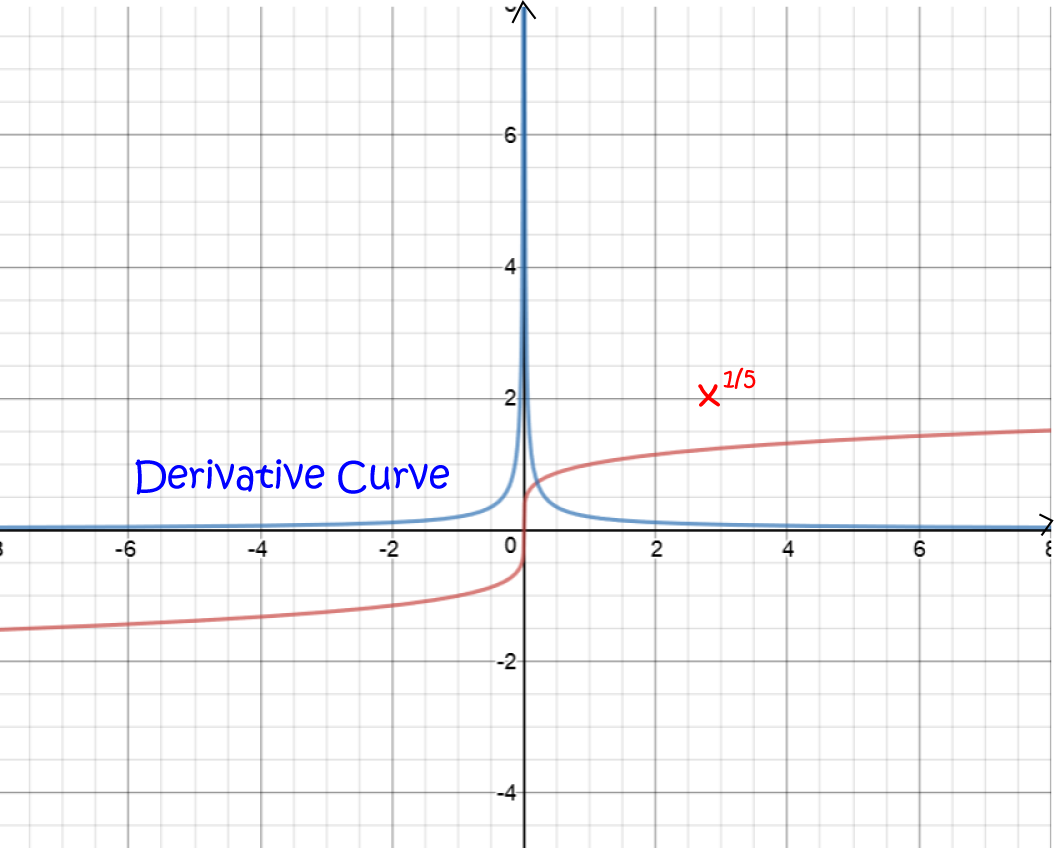
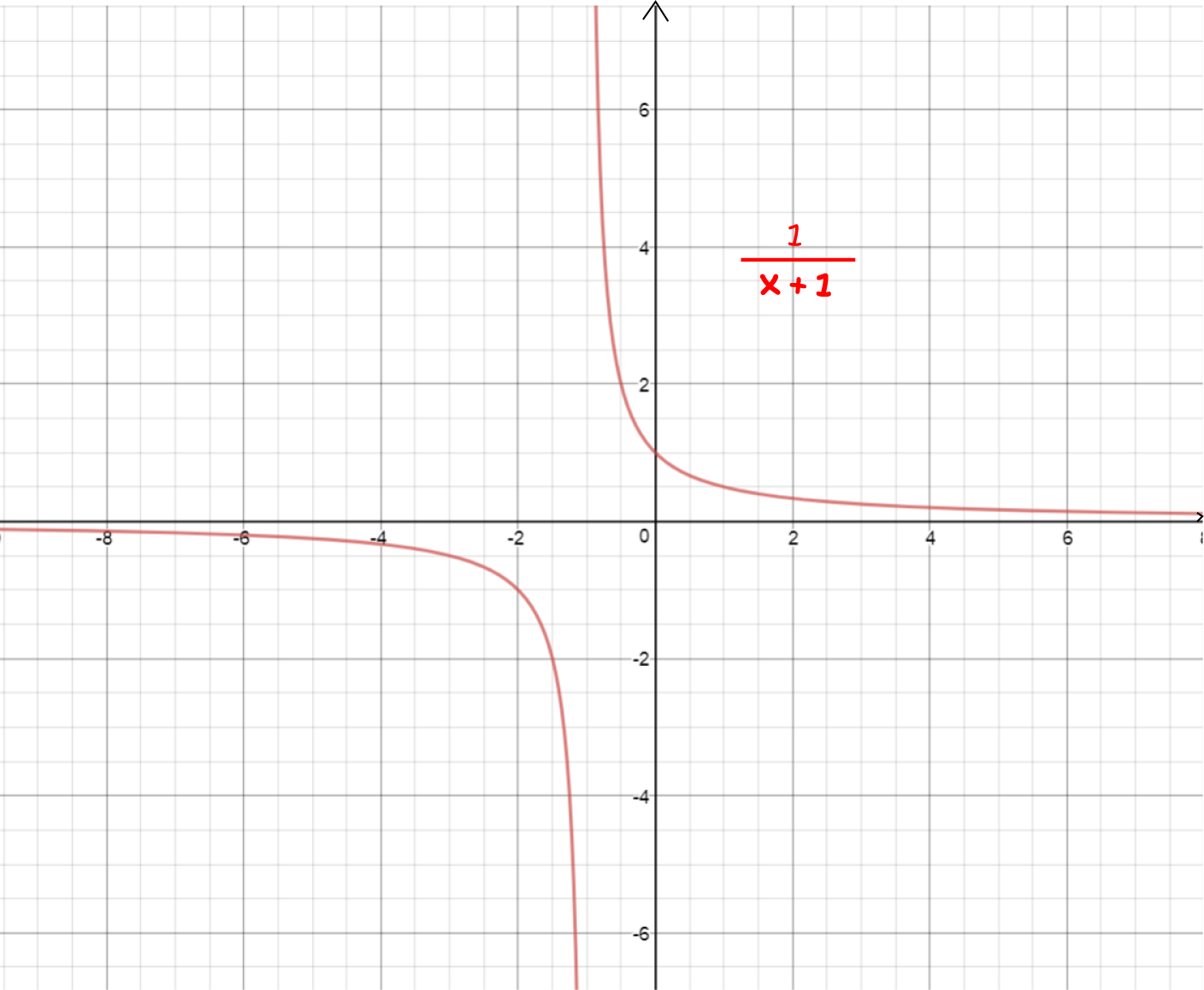
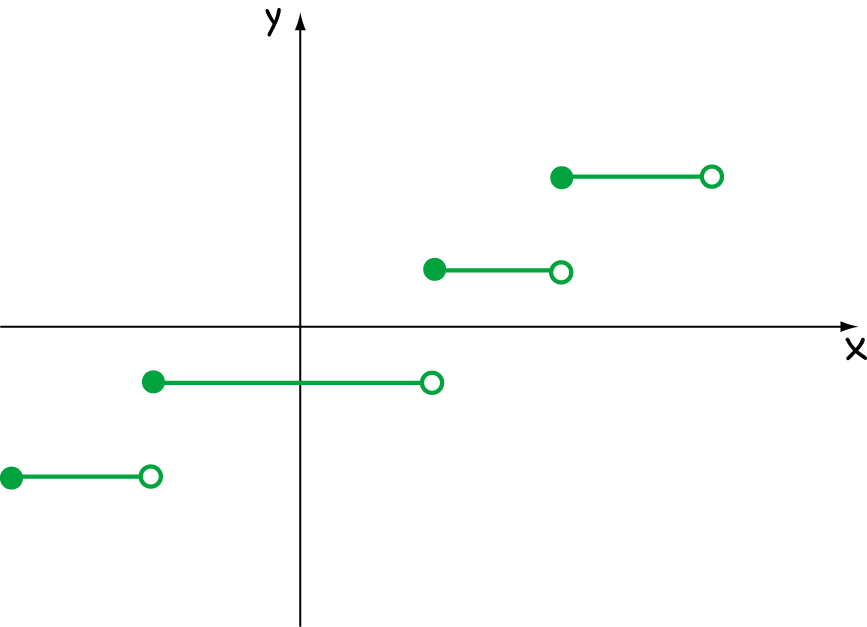
What Is Differentiable Calculus - Let's have another look at our first example: We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx. Let's have another look at our first example:
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx. Let's have another look at our first example:
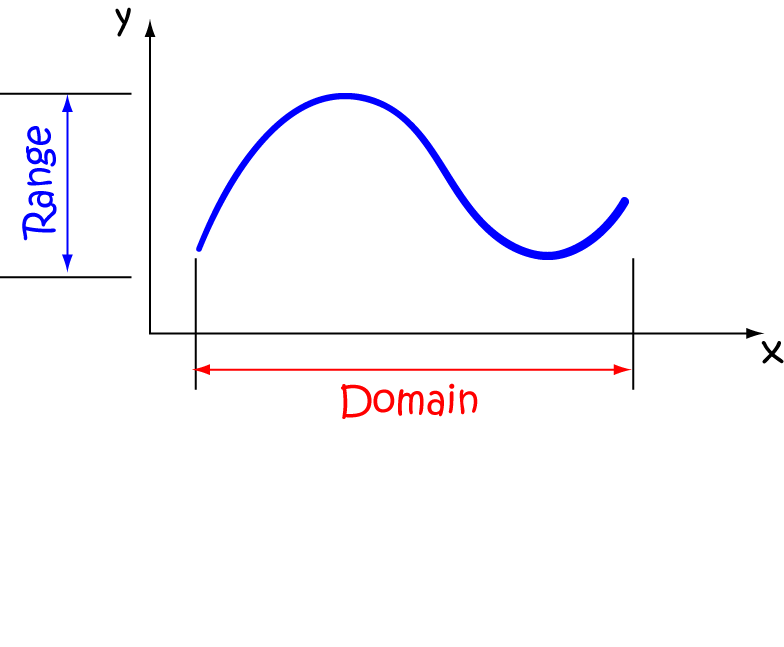
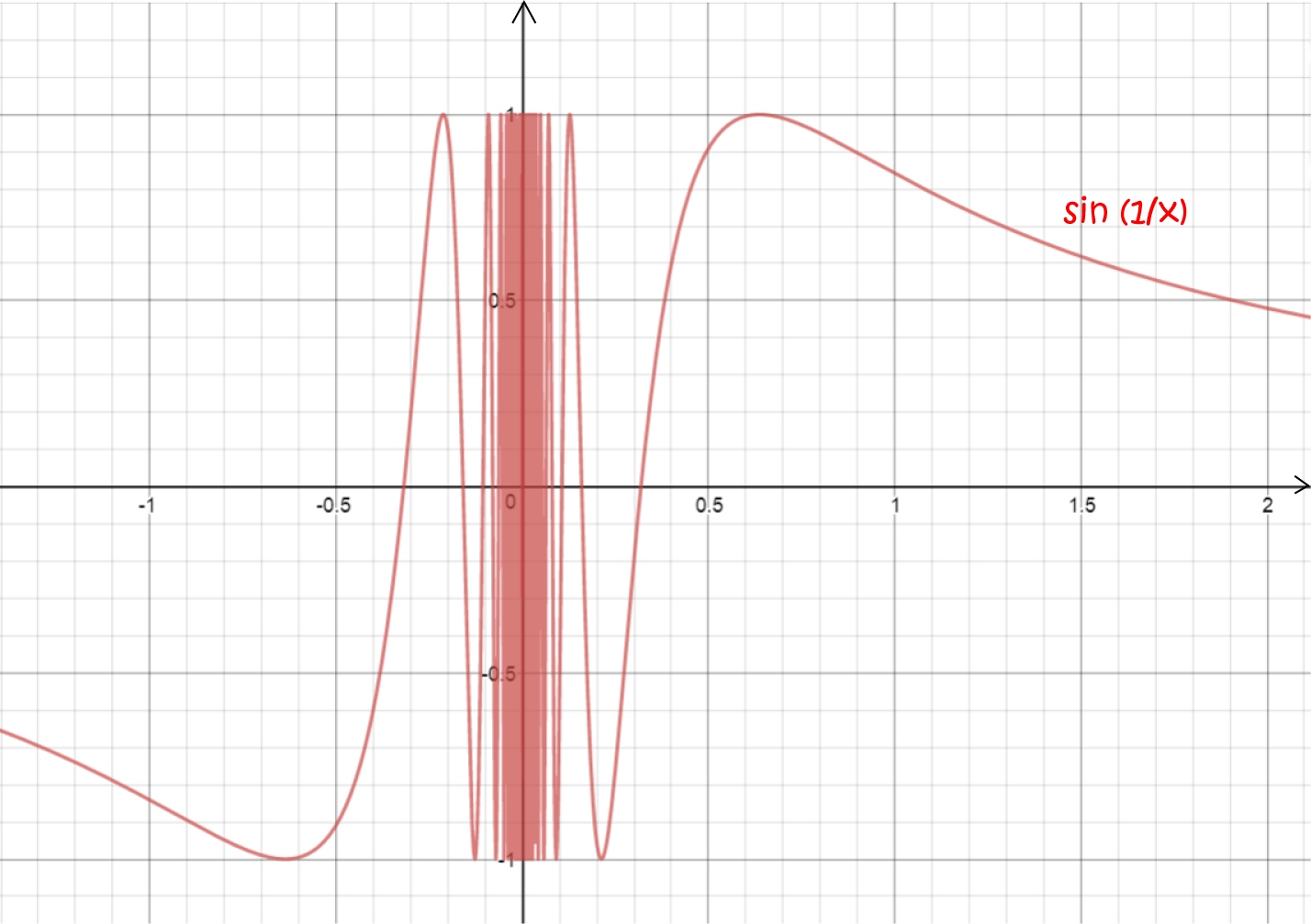
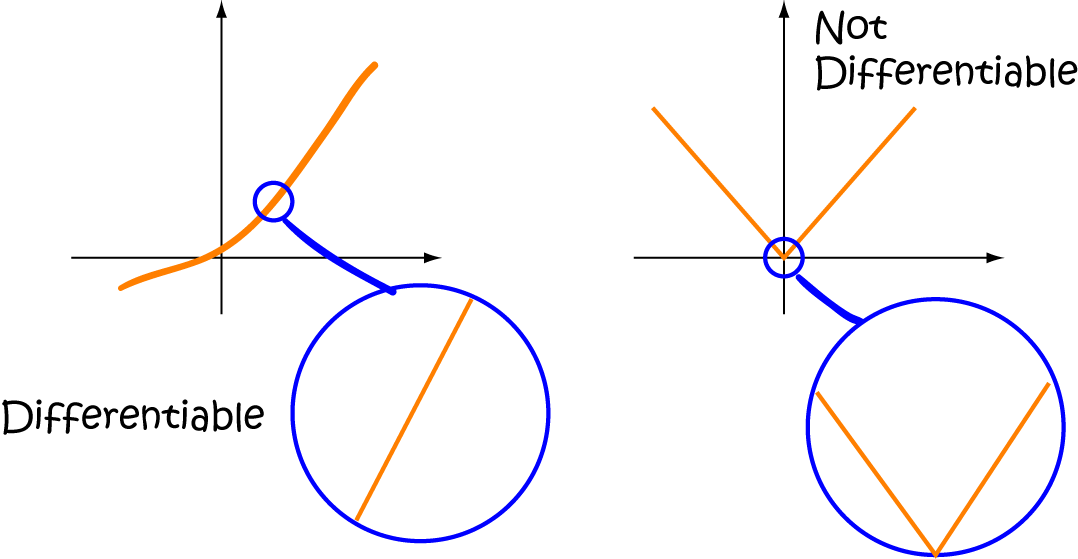
Differentiable vs. Continuous Functions Understanding the Distinctions
Let's have another look at our first example: We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
What does it mean for a function to be differentiable? Calculus
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx. Let's have another look at our first example:
Differentiable function Wikiwand
Let's have another look at our first example: We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
Differential Calculus Terms, Formulas, Rules, Examples
Let's have another look at our first example: We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
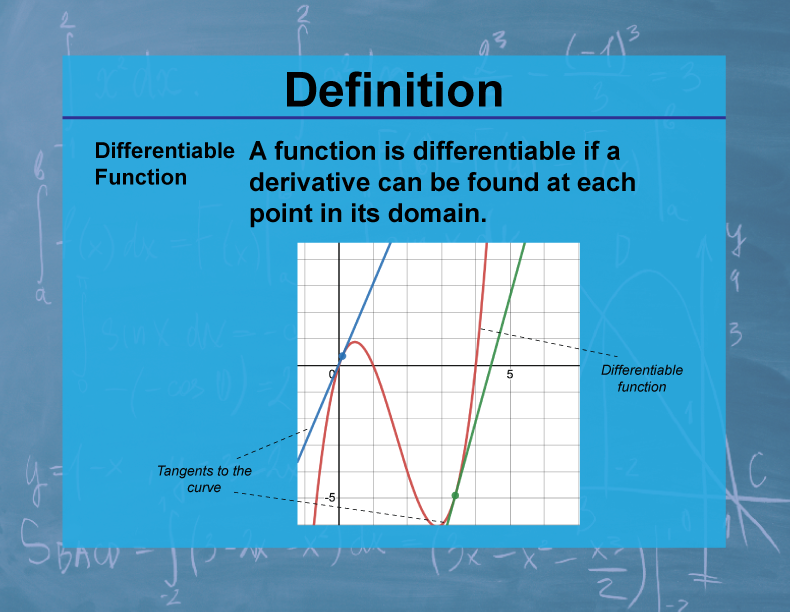
DefinitionCalculus TopicsDifferentiable Function Media4Math
Let's have another look at our first example: We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
What does it mean for a function to be differentiable? Calculus
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx. Let's have another look at our first example:
What does it mean for a function to be differentiable? Calculus
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx. Let's have another look at our first example:
What does it mean for a function to be differentiable? Calculus
Let's have another look at our first example: We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
What does it mean for a function to be differentiable? Calculus
We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx. Let's have another look at our first example:
What does it mean for a function to be differentiable? Calculus
Let's have another look at our first example: We studied differentials in section 4.4, where definition 18 states that if y = f(x) and f is differentiable, then dy = f ′ (x)dx.
We Studied Differentials In Section 4.4, Where Definition 18 States That If Y = F(X) And F Is Differentiable, Then Dy = F ′ (X)Dx.
Let's have another look at our first example: