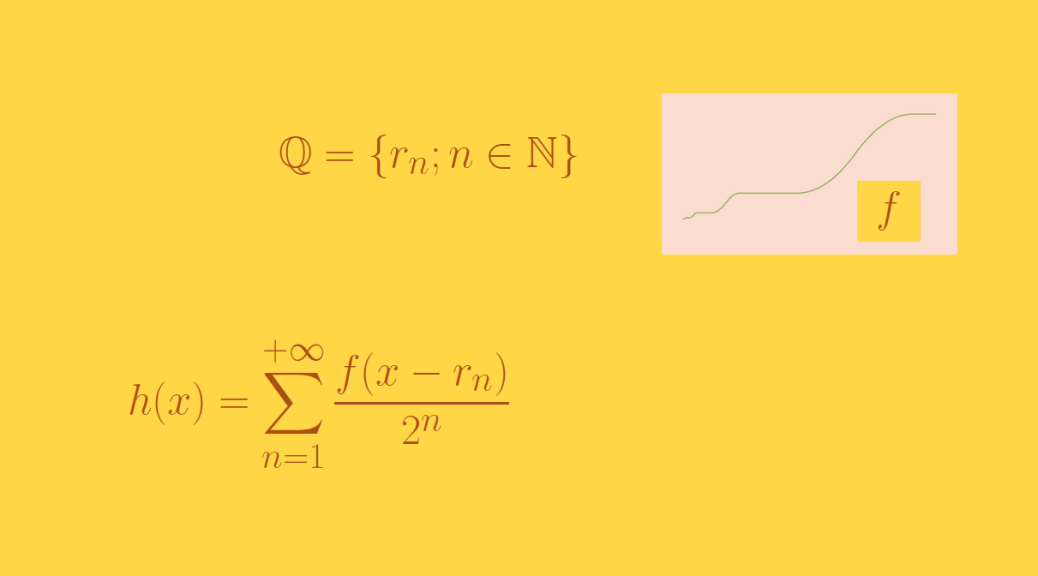Totally Differentiable - The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. Total differentials can be generalized. Let \(dx\), \(dy\) and \(dz\) represent changes. The total differential gives an approximation of the change in z given small changes in x and y. We can use this to approximate error propagation;.
For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Total differentials can be generalized. Let \(dx\), \(dy\) and \(dz\) represent changes. The total differential gives an approximation of the change in z given small changes in x and y. We can use this to approximate error propagation;.
We can use this to approximate error propagation;. Let \(dx\), \(dy\) and \(dz\) represent changes. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Total differentials can be generalized. The total differential gives an approximation of the change in z given small changes in x and y. For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f.
A continuous function not differentiable at the rationals but
For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. The total differential gives an approximation of the change in z given small changes in x and y. We can use this to approximate error propagation;. Let \(dx\), \(dy\) and \(dz\) represent changes. Total differentials can be generalized.
Differentiable vs. Continuous Functions Understanding the Distinctions
For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Let \(w=f(x,y,z)\) be continuous on an open set \(s\)..
Differentiable Programming A Simple Introduction
For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Let \(dx\), \(dy\) and \(dz\) represent changes. Total differentials can be generalized. The former part of δ x is called the (total) differential or the exact differential of the.
Differentiable Font download free
Total differentials can be generalized. The total differential gives an approximation of the change in z given small changes in x and y. We can use this to approximate error propagation;. Let \(dx\), \(dy\) and \(dz\) represent changes. Let \(w=f(x,y,z)\) be continuous on an open set \(s\).
DefinitionCalculus TopicsDifferentiable Function Media4Math
For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Let \(dx\), \(dy\) and \(dz\) represent changes. Total differentials.
Differentiable function Wikiwand
For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. The total differential gives an approximation of the change in z given small changes in x and y. We can use this to approximate error propagation;. The former part of δ x is called the (total) differential or.
Continuous but Nowhere Differentiable Math Fun Facts
Total differentials can be generalized. The total differential gives an approximation of the change in z given small changes in x and y. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Let \(dx\), \(dy\) and \(dz\) represent changes. We can use this to approximate error propagation;.
Differentiable Turbulence Paper and Code CatalyzeX
Total differentials can be generalized. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). We can use this to approximate error propagation;. Let \(dx\), \(dy\) and \(dz\) represent changes. For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f.
Solved A5. Prove that if f D → R2 is totally
The total differential gives an approximation of the change in z given small changes in x and y. We can use this to approximate error propagation;. For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. The former part of δ x is called the (total) differential or.
PPT Differentiable functions are Continuous PowerPoint Presentation
We can use this to approximate error propagation;. Let \(dx\), \(dy\) and \(dz\) represent changes. The former part of δ x is called the (total) differential or the exact differential of the function f in the point (x, y, z) and it is denoted. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). For a function f = f(x,y,z).
Total Differentials Can Be Generalized.
Let \(dx\), \(dy\) and \(dz\) represent changes. For a function f = f(x,y,z) whose partial derivatives exists, the total differential of f is given by df = f. We can use this to approximate error propagation;. The total differential gives an approximation of the change in z given small changes in x and y.
The Former Part Of Δ X Is Called The (Total) Differential Or The Exact Differential Of The Function F In The Point (X, Y, Z) And It Is Denoted.
Let \(w=f(x,y,z)\) be continuous on an open set \(s\).