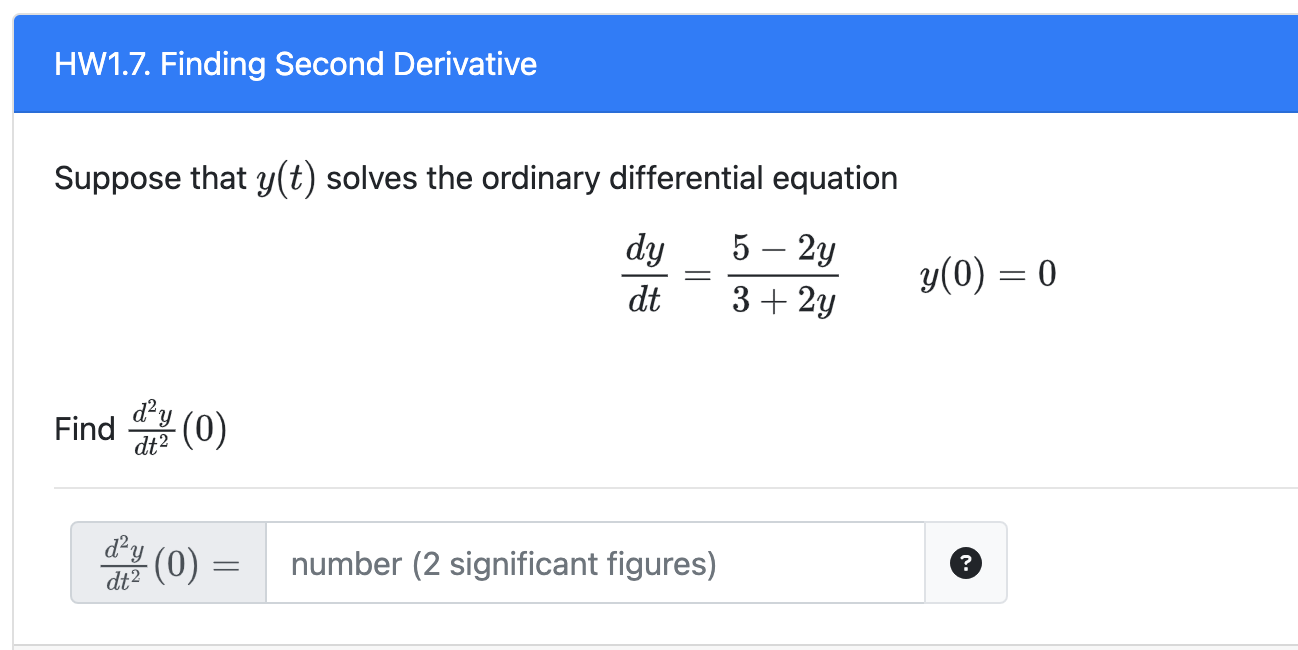
Suppose That Solves The Ordinary Differential Equation Find - To find (d^2 y / dt^2) (0), we. D t d y = 5 + 2 y 4 − 3 y , y (0) = 0. Explore analysis with applications to dilution models. Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? Find y(1) i tried solving using separable. Solutions of differential equations an (ordinary) differential equation is an equation involving a function and its derivatives. 5 y (0) = 1 = find y (1) y (1) number (2 significant figures) ?. Suppose that y(t) solves the ordinary differential equation. To find the second derivative of y (t) at t = 0, we start with the given ordinary differential equation (ode):
Suppose that y(t) solves the ordinary differential equation. D t d y = 5 + 2 y 4 − 3 y , y (0) = 0. To find the second derivative of y (t) at t = 0, we start with the given ordinary differential equation (ode): To find (d^2 y / dt^2) (0), we. Solutions of differential equations an (ordinary) differential equation is an equation involving a function and its derivatives. Explore analysis with applications to dilution models. Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? 5 y (0) = 1 = find y (1) y (1) number (2 significant figures) ?. Find y(1) i tried solving using separable.
D t d y = 5 + 2 y 4 − 3 y , y (0) = 0. To find (d^2 y / dt^2) (0), we. Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? To find the second derivative of y (t) at t = 0, we start with the given ordinary differential equation (ode): Find y(1) i tried solving using separable. Suppose that y(t) solves the ordinary differential equation. 5 y (0) = 1 = find y (1) y (1) number (2 significant figures) ?. Explore analysis with applications to dilution models. Solutions of differential equations an (ordinary) differential equation is an equation involving a function and its derivatives.
Solved 1. Give an example of an ordinary differential
To find (d^2 y / dt^2) (0), we. Suppose that y(t) solves the ordinary differential equation. Solutions of differential equations an (ordinary) differential equation is an equation involving a function and its derivatives. Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? Explore analysis with applications to dilution models.
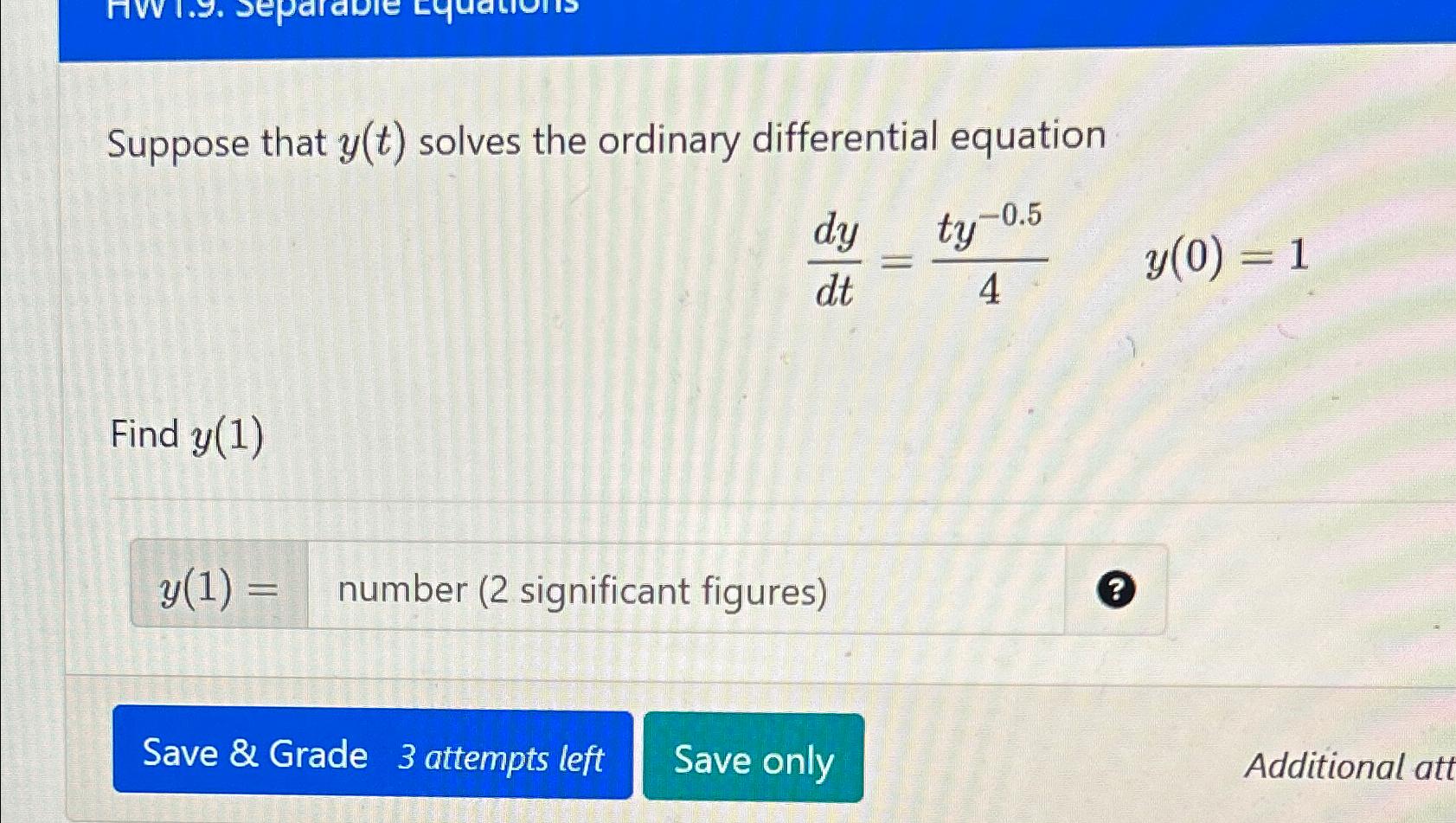
Solved HW1.9. Separable Equations Suppose that y(t) solves
To find the second derivative of y (t) at t = 0, we start with the given ordinary differential equation (ode): Suppose that y(t) solves the ordinary differential equation. Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? D t d y = 5 + 2 y 4 − 3 y , y (0) =.
Finding The Solution Suppose That Solves The Ordinary Differential
Solutions of differential equations an (ordinary) differential equation is an equation involving a function and its derivatives. Suppose that y(t) solves the ordinary differential equation. Find y(1) i tried solving using separable. 5 y (0) = 1 = find y (1) y (1) number (2 significant figures) ?. D t d y = 5 + 2 y 4 − 3.
Solved Suppose that y(t) solves the ordinary differential
Find y(1) i tried solving using separable. Solutions of differential equations an (ordinary) differential equation is an equation involving a function and its derivatives. 5 y (0) = 1 = find y (1) y (1) number (2 significant figures) ?. Suppose that y(t) solves the ordinary differential equation. To find (d^2 y / dt^2) (0), we.
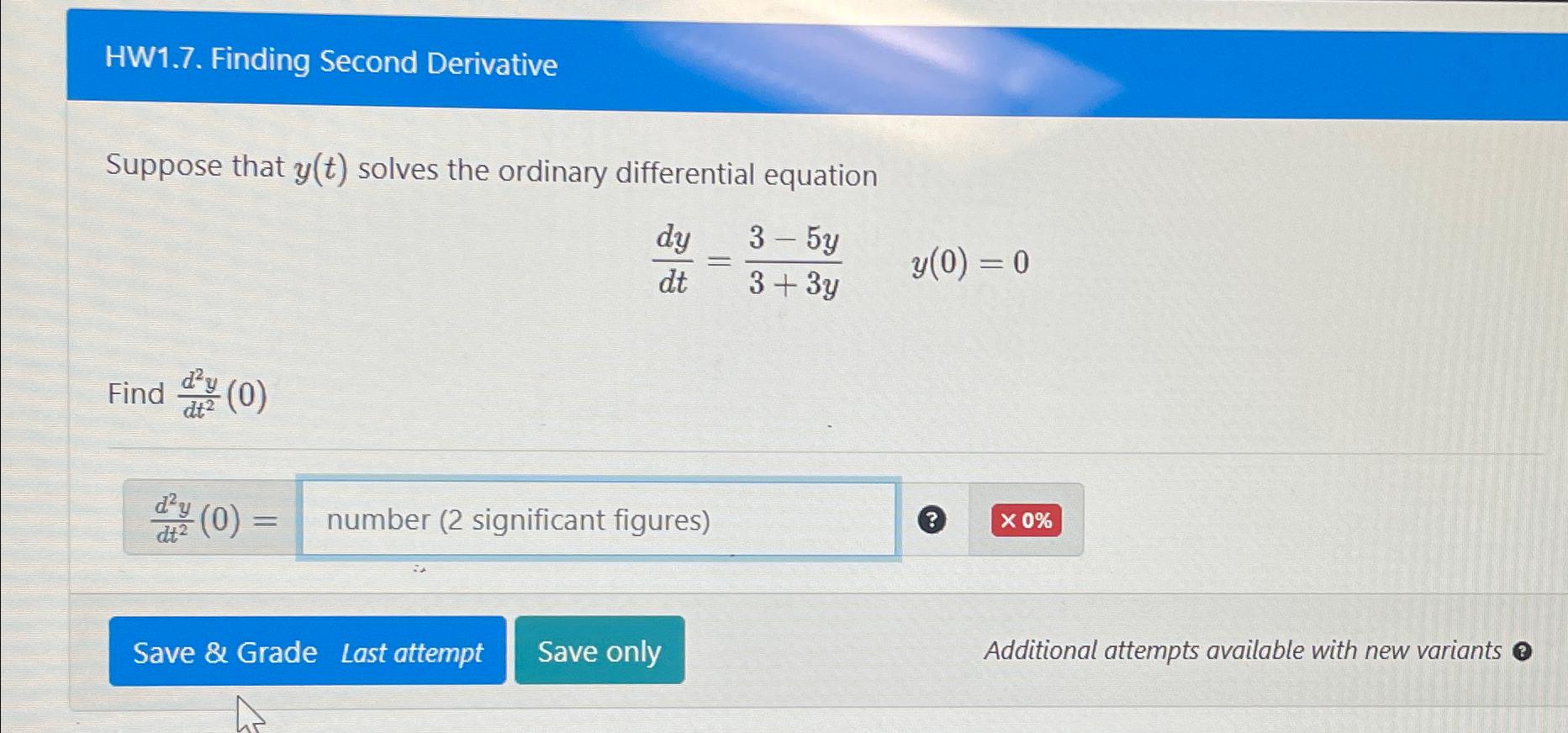
Solved HW1.7. Finding Second DerivativeSuppose that y(t)
Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? Solutions of differential equations an (ordinary) differential equation is an equation involving a function and its derivatives. To find the second derivative of y (t) at t = 0, we start with the given ordinary differential equation (ode): To find (d^2 y / dt^2) (0), we..
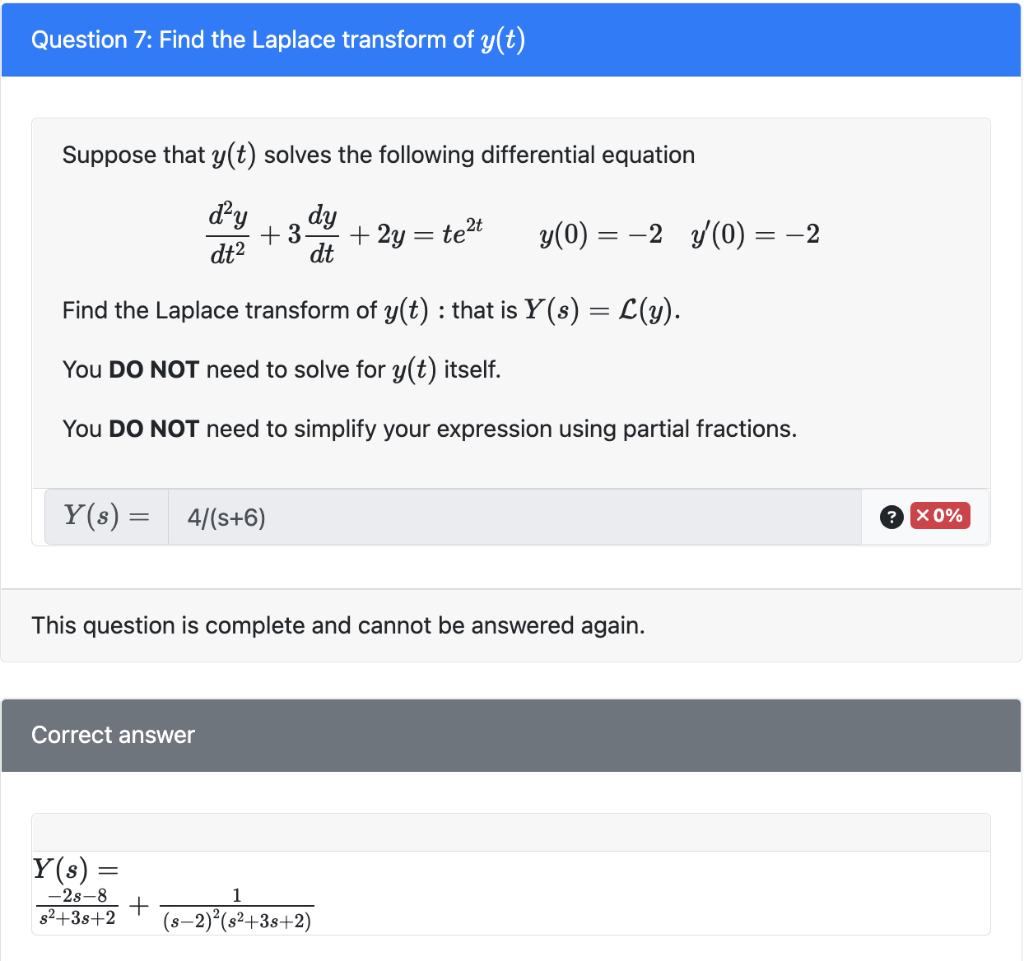
SOLVED "Could you please solve this question immediately? (20 pts
Solutions of differential equations an (ordinary) differential equation is an equation involving a function and its derivatives. 5 y (0) = 1 = find y (1) y (1) number (2 significant figures) ?. To find (d^2 y / dt^2) (0), we. Find y(1) i tried solving using separable. Suppose that y(t) solves the ordinary differential equation.
Solved Suppose that y(t) solves the following differential
To find the second derivative of y (t) at t = 0, we start with the given ordinary differential equation (ode): Find y(1) i tried solving using separable. 5 y (0) = 1 = find y (1) y (1) number (2 significant figures) ?. D t d y = 5 + 2 y 4 − 3 y , y (0).
Solved Suppose that y(t) solves the ordinary differential
Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? 5 y (0) = 1 = find y (1) y (1) number (2 significant figures) ?. D t d y = 5 + 2 y 4 − 3 y , y (0) = 0. Find y(1) i tried solving using separable. Suppose that y(t) solves the.
Solved Suppose that y(t) solves the ordinary differential
Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? D t d y = 5 + 2 y 4 − 3 y , y (0) = 0. To find (d^2 y / dt^2) (0), we. Explore analysis with applications to dilution models. Solutions of differential equations an (ordinary) differential equation is an equation involving a.
Solution to ordinary differential equation. Download Scientific Diagram
Find y(1) i tried solving using separable. 5 y (0) = 1 = find y (1) y (1) number (2 significant figures) ?. Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? To find the second derivative of y (t) at t = 0, we start with the given ordinary differential equation (ode): To find.
5 Y (0) = 1 = Find Y (1) Y (1) Number (2 Significant Figures) ?.
Separable equations suppose that y (t) solves the ordinary differential equation dy dt ty? Suppose that y(t) solves the ordinary differential equation. Solutions of differential equations an (ordinary) differential equation is an equation involving a function and its derivatives. Find y(1) i tried solving using separable.
To Find (D^2 Y / Dt^2) (0), We.
D t d y = 5 + 2 y 4 − 3 y , y (0) = 0. To find the second derivative of y (t) at t = 0, we start with the given ordinary differential equation (ode): Explore analysis with applications to dilution models.