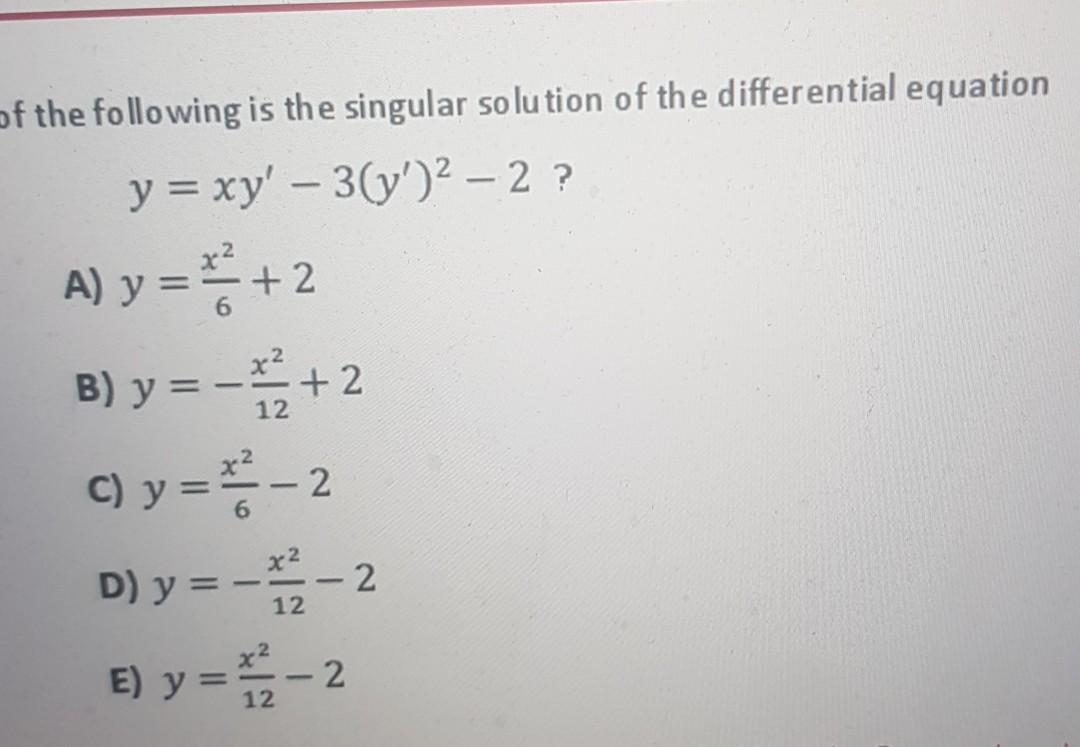Singular Solution Of Differential Equation - A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. Learn how to identify and solve singular solutions of separable differential equations. See examples with critical points, equilibrium solutions and.
A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. Learn how to identify and solve singular solutions of separable differential equations. See examples with critical points, equilibrium solutions and. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where.
A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. See examples with critical points, equilibrium solutions and. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. Learn how to identify and solve singular solutions of separable differential equations.
[Solved] Determine singular points, of each differential equation and
See examples with critical points, equilibrium solutions and. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. Learn how to identify and solve singular solutions of separable differential equations.
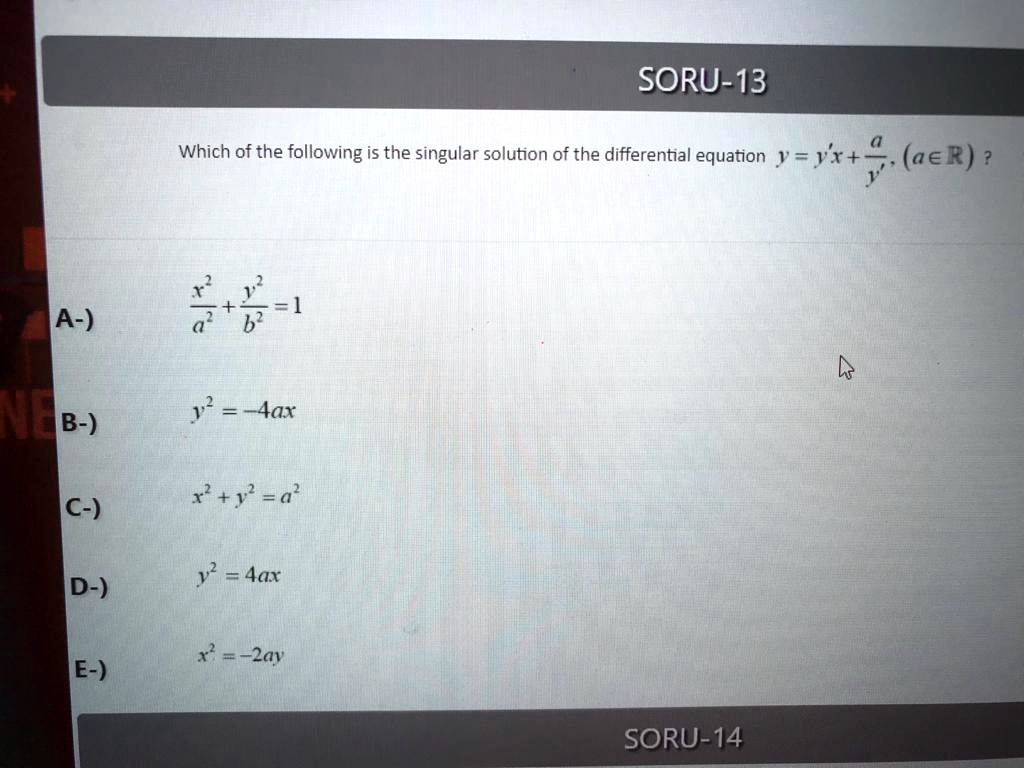
SOLVED 'singular solution SORU13 Which of the following is the
A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. See examples with critical points, equilibrium solutions and. Learn how to identify and solve singular solutions of separable differential equations. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where.
[Solved] . Find all Singular points of the given differential equation
If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. See examples with critical points, equilibrium solutions and. Learn how to identify and solve singular solutions of separable differential equations. A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of.
Solved which of the following is the singular solution of
Learn how to identify and solve singular solutions of separable differential equations. See examples with critical points, equilibrium solutions and. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of.
[Solved] Determine the singular points of the given differential
A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. Learn how to identify and solve singular solutions of separable differential equations. See examples with critical points, equilibrium solutions and.
(PDF) Singular solutions of a singular differential equation
A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. See examples with critical points, equilibrium solutions and. Learn how to identify and solve singular solutions of separable differential equations.
(PDF) Existence of positive solution for singular fractional
See examples with critical points, equilibrium solutions and. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. Learn how to identify and solve singular solutions of separable differential equations.
Solved of the following is the singular solution of the
Learn how to identify and solve singular solutions of separable differential equations. See examples with critical points, equilibrium solutions and. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of.
[Solved] Determine singular points, of each differential equation and
See examples with critical points, equilibrium solutions and. Learn how to identify and solve singular solutions of separable differential equations. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of.
SOLVEDA singular solution of a differential equation is a solution
A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where. Learn how to identify and solve singular solutions of separable differential equations. See examples with critical points, equilibrium solutions and.
See Examples With Critical Points, Equilibrium Solutions And.
Learn how to identify and solve singular solutions of separable differential equations. A solution of the differential equation (1) which cannot be obtained from the general integral, is called a singular solution of. If your given differential equation is of clairaut's form, i.e., of the form $$y=px+f(p)\qquad \text{where.