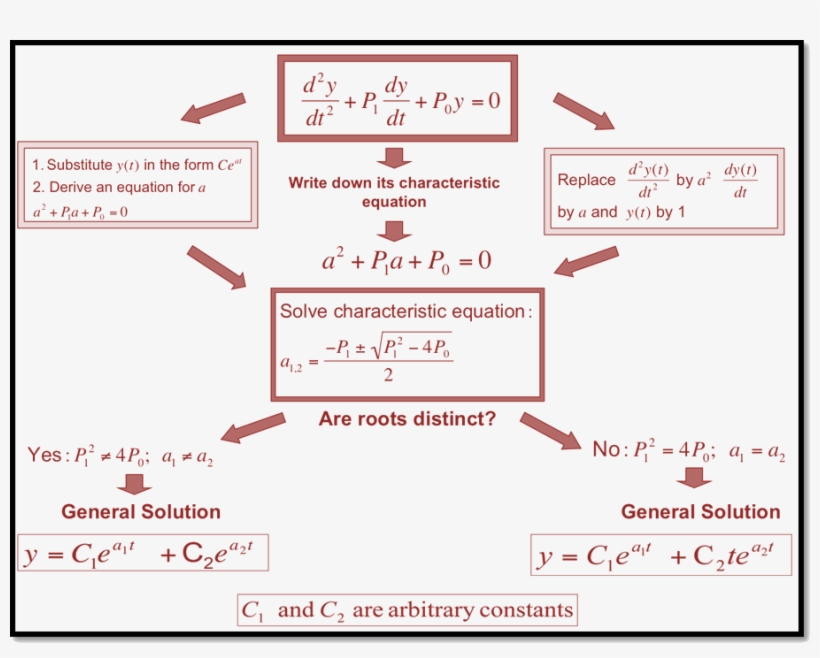
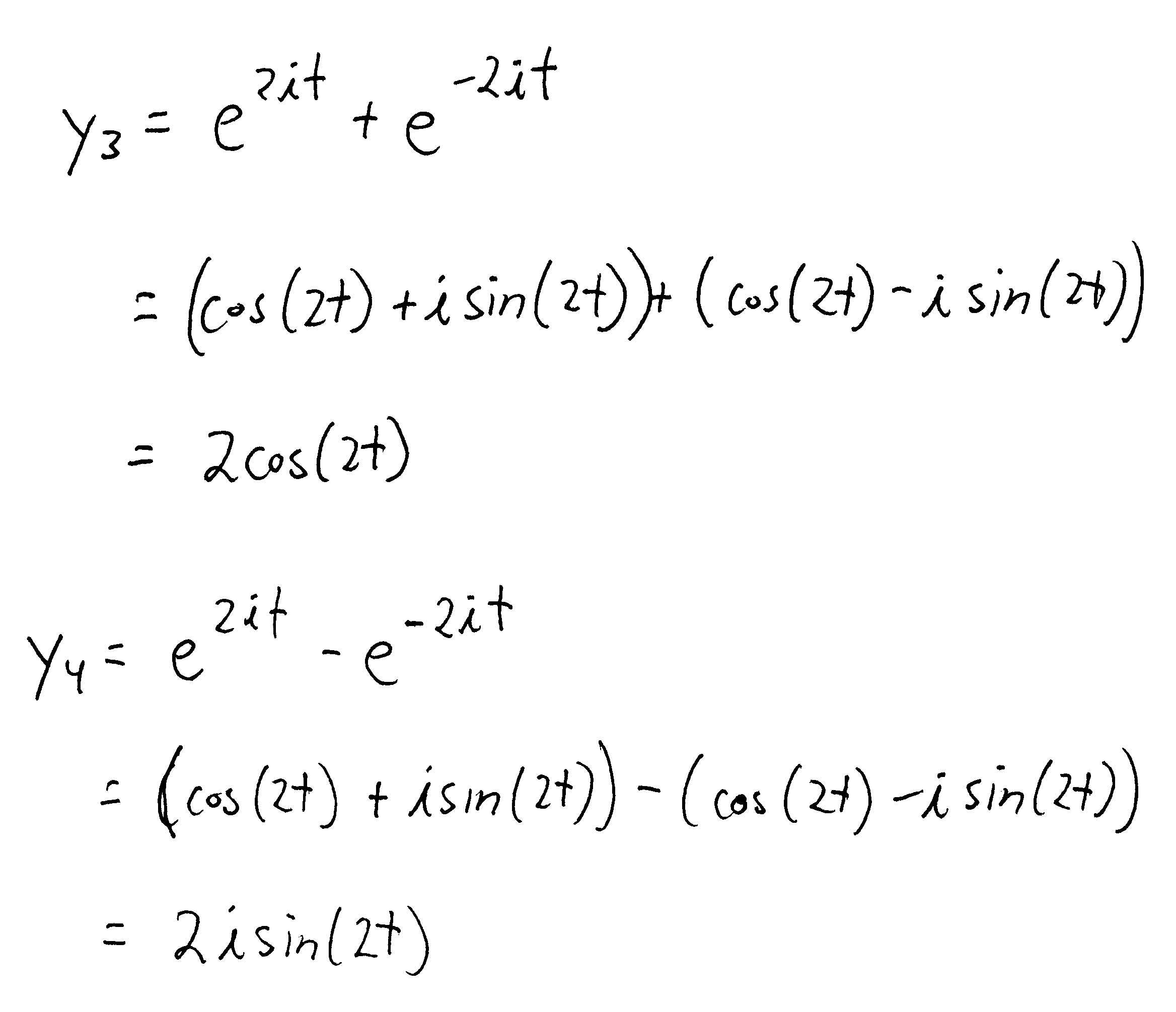Second Order Ordinary Differential Equation Solution - Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.
Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.
Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.
PPT Numerical Solution of Ordinary Differential Equation PowerPoint
The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.
Solved Problem 10.1 FirstOrder Ordinary Differential
Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.
College Park Tutors Blog Differential Equations Solving a second
Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.
A Complete Guide to Understanding Second Order Differential Equations
The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.
[Solved] The general solution to the secondorder differential equation
The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.
Solution Of Second Order Differential Equation Differential Equation
The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.
Solving Second Order Differential Equation Images and Photos finder
The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.
Finding a second solution to a 2nd order differential equation
Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.
Example 4.2.2 (SecondOrder Ordinary Differential
Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒. The solution of these equations is achieved in stages.
First Order Differential Equation Worksheet Equations Worksheets
The solution of these equations is achieved in stages. Corresponding second order ode’s are obtained by taking another derivative, as x =tant, ⇒ x˙ =1+x2, ⇒ x¨ =2xx˙ =2x(1+x2), (1.3.17) and x =tanht, ⇒.
Corresponding Second Order Ode’s Are Obtained By Taking Another Derivative, As X =Tant, ⇒ X˙ =1+X2, ⇒ X¨ =2Xx˙ =2X(1+X2), (1.3.17) And X =Tanht, ⇒.
The solution of these equations is achieved in stages.