Power Series Differentiation And Integration - When a power series converges, it defines a function. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. We show how to do this in the next two examples. Let's do calculus on this function. The derivative of the power series exists and is. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible.
Let's do calculus on this function. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. We show how to do this in the next two examples. When a power series converges, it defines a function. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. The derivative of the power series exists and is.
We show how to do this in the next two examples. Let's do calculus on this function. When a power series converges, it defines a function. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. The derivative of the power series exists and is. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible.
Differentiation and Integration of Power Series DocsLib
We show how to do this in the next two examples. When a power series converges, it defines a function. Let's do calculus on this function. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. To use the geometric series formula, the function must be able to be put.
Power Series PDF
When a power series converges, it defines a function. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. We show how to do this in the next.
Differentiation and Integration Mean Green Math
The derivative of the power series exists and is. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. We show how to do this in the next two examples. When a power series converges, it defines a function. To use the geometric series formula, the function must be able.
Power series differentiation to find the function's representation
Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. Let's do calculus on this function. When a power series converges, it defines a function. We show how.
Power series differentiation to find the function's representation
The derivative of the power series exists and is. Let's do calculus on this function. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. We show how.
Power Series PDF
To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. When a power series converges, it defines a function. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. We show how to do this in the next.
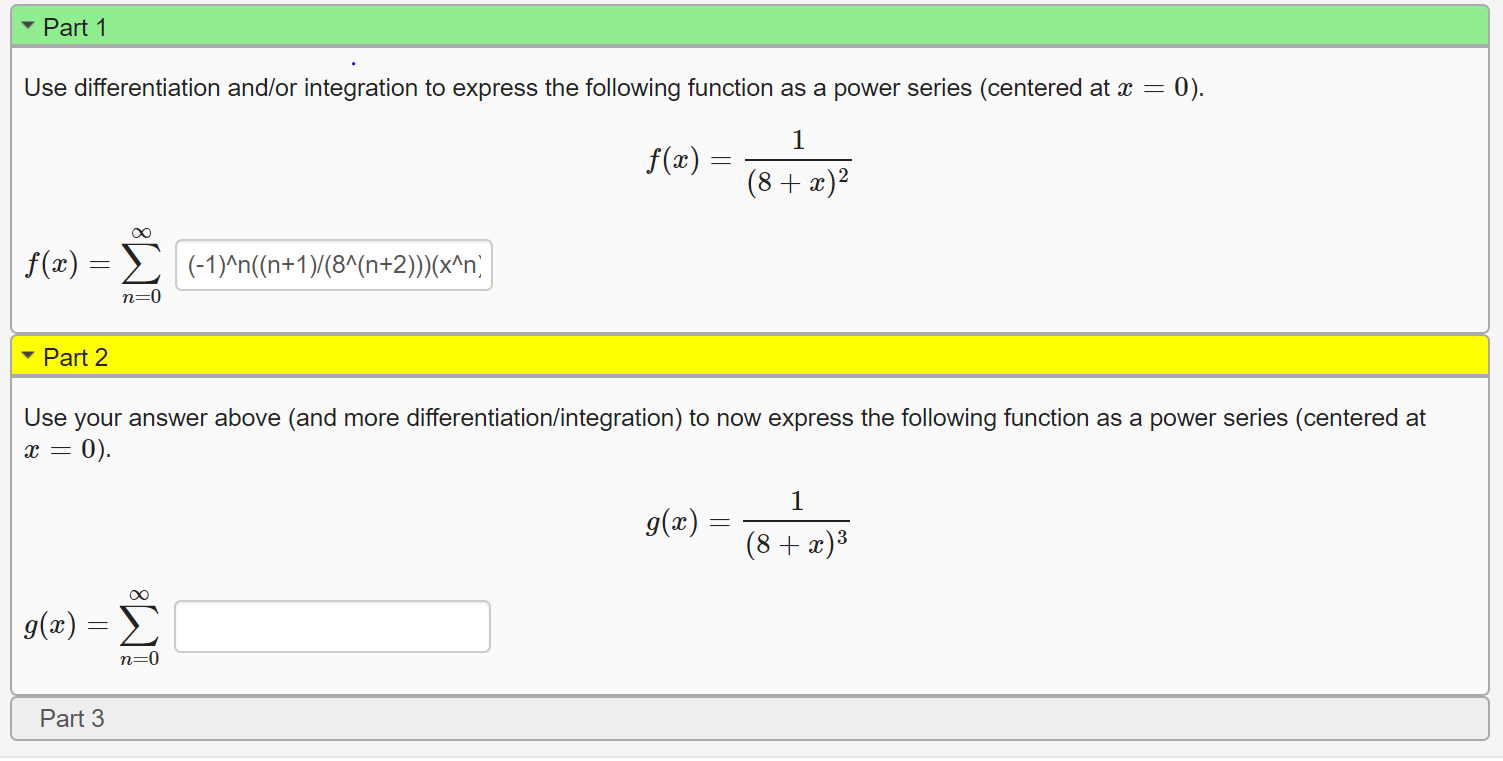
Solved Part 1 Use differentiation and/or integration to
The derivative of the power series exists and is. Let's do calculus on this function. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. When a power.
13.Differentiation and Integration of Power Series.pdf Power Series
We show how to do this in the next two examples. Let's do calculus on this function. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many. When.
Solved 33 Power Series Differentiation and Integration
The derivative of the power series exists and is. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. When a power series converges, it defines a function. Power series diff and integ geometric series radius of convergence variations on the geometric series (i) closed forms for many..
Solved Part 1 Use differentiation and/or integration to
Let's do calculus on this function. The derivative of the power series exists and is. When a power series converges, it defines a function. We show how to do this in the next two examples. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible.
Power Series Diff And Integ Geometric Series Radius Of Convergence Variations On The Geometric Series (I) Closed Forms For Many.
Let's do calculus on this function. To use the geometric series formula, the function must be able to be put into a specific form, which is often impossible. We show how to do this in the next two examples. When a power series converges, it defines a function.