Perfect Differential - Find the perfect differential of the following: A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max{∂p (s) : Exact differential we work in two dimensions, with similar definitions holding in any other number of dimensions. In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max {∂p (s) : I differentiated the first term with respect.
A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max{∂p (s) : In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max {∂p (s) : Find the perfect differential of the following: Exact differential we work in two dimensions, with similar definitions holding in any other number of dimensions. I differentiated the first term with respect.
Exact differential we work in two dimensions, with similar definitions holding in any other number of dimensions. A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. Find the perfect differential of the following: In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max {∂p (s) : In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max{∂p (s) : I differentiated the first term with respect.
Application of Differential Equation
A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. Find the perfect differential of the following: Exact differential we work in two dimensions, with similar definitions holding in any other number of dimensions. I differentiated the first term with respect. In this paper, we introduce the study of.
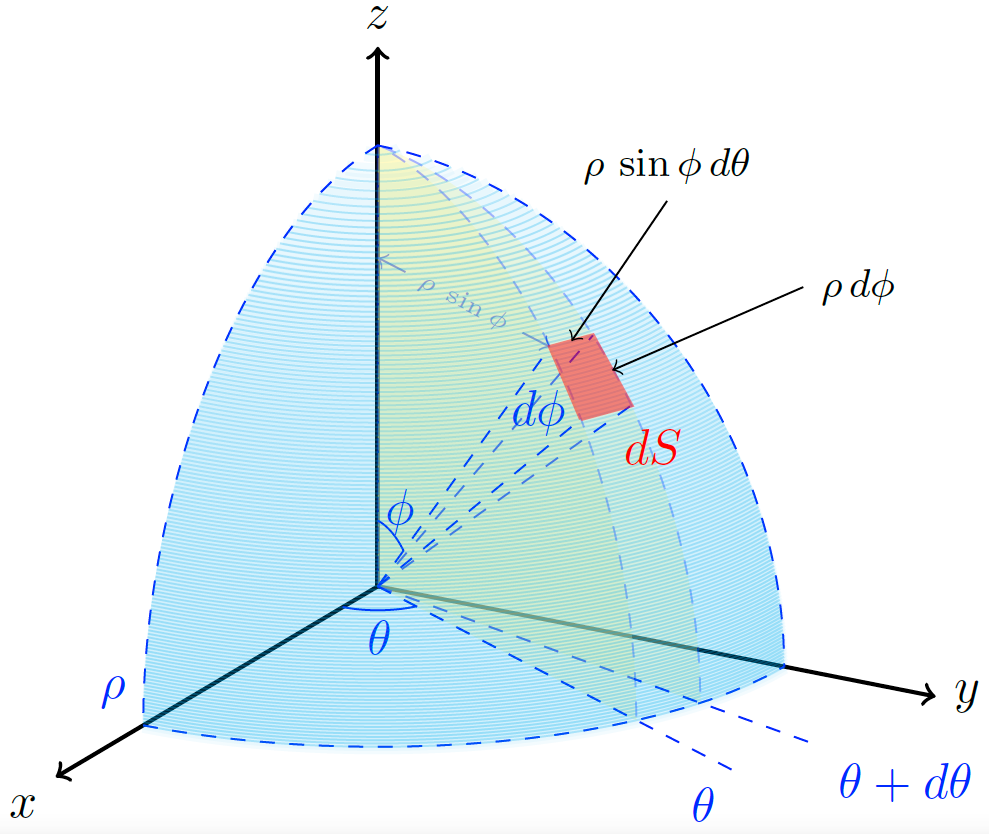
Differential of Surface Area Spherical Coordinates
A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. Find the perfect differential of the following: Exact differential we work in two dimensions, with similar definitions holding in any other number of dimensions. In this paper, we introduce the study of the perfect differential of a graph, which.
(PDF) On the Perfect Differential of a Graph
A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max{∂p (s) : I differentiated the first term with respect. Exact differential we work in two dimensions, with.
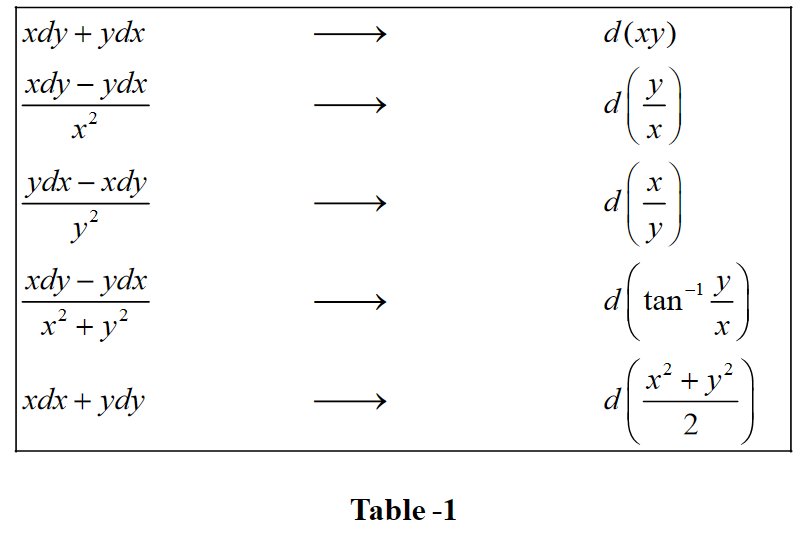
Examples On Exact Differential Equations What is Examples On Exact
Exact differential we work in two dimensions, with similar definitions holding in any other number of dimensions. In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max{∂p (s) : A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space.
DIFFERENTIAL PRESSURE GAUGE Hydair
In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max{∂p (s) : Find the perfect differential of the following: I differentiated the first term with respect. A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. In.
Differential Equation Meaning, Types, Order, Degree & Solution Cuemath
In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max {∂p (s) : A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. In this paper, we introduce the study of the perfect differential of a graph,.
Differential Equations (Definition, Types, Order, Degree, Examples)
In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max {∂p (s) : Exact differential we work in two dimensions, with similar definitions holding in any other number of dimensions. In this paper, we introduce the study of the perfect differential of a graph, which we define as.
(PDF) Approximate perfect differential equations of second order
In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max{∂p (s) : Find the perfect differential of the following: In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max {∂p (s) : A perfect differential ideal.
Comparing differential abundance detection tools in the presence of
A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. I differentiated the first term with respect. In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max {∂p (s) : In this paper, we introduce the study.
(PDF) From differential and perfect differential to Roman domination
I differentiated the first term with respect. In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max{∂p (s) : Exact differential we work in two dimensions, with similar definitions holding in any other number of dimensions. A perfect differential ideal corresponds to a differential algebraic variety — the.
I Differentiated The First Term With Respect.
Exact differential we work in two dimensions, with similar definitions holding in any other number of dimensions. In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max {∂p (s) : A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some. In this paper, we introduce the study of the perfect differential of a graph, which we define as ∂p (g) = max{∂p (s) :