Parabolic Differential Equation - (6.1) ut = ∆u + f is a prototypical example of a parabolic pde. If b2 4ac = 0, then the pde is parabolic (heat). Tumor growth models describe the diffusion of cancer cells through the tissue. If b2 4ac > 0, then the pde is hyperbolic (wave). This pde has to be.
This pde has to be. (6.1) ut = ∆u + f is a prototypical example of a parabolic pde. If b2 4ac = 0, then the pde is parabolic (heat). If b2 4ac > 0, then the pde is hyperbolic (wave). Tumor growth models describe the diffusion of cancer cells through the tissue.
If b2 4ac = 0, then the pde is parabolic (heat). Tumor growth models describe the diffusion of cancer cells through the tissue. This pde has to be. If b2 4ac > 0, then the pde is hyperbolic (wave). (6.1) ut = ∆u + f is a prototypical example of a parabolic pde.
(PDF) Structure of a Parabolic Partial Differential Equation on Graphs
Tumor growth models describe the diffusion of cancer cells through the tissue. If b2 4ac > 0, then the pde is hyperbolic (wave). This pde has to be. If b2 4ac = 0, then the pde is parabolic (heat). (6.1) ut = ∆u + f is a prototypical example of a parabolic pde.
Parabolic Partial Differential Equation from Wolfram MathWorld
(6.1) ut = ∆u + f is a prototypical example of a parabolic pde. This pde has to be. If b2 4ac = 0, then the pde is parabolic (heat). Tumor growth models describe the diffusion of cancer cells through the tissue. If b2 4ac > 0, then the pde is hyperbolic (wave).
Localized orthogonal for a multiscale parabolic
If b2 4ac = 0, then the pde is parabolic (heat). Tumor growth models describe the diffusion of cancer cells through the tissue. This pde has to be. If b2 4ac > 0, then the pde is hyperbolic (wave). (6.1) ut = ∆u + f is a prototypical example of a parabolic pde.
Solved a) Classify the given partial differential equation
Tumor growth models describe the diffusion of cancer cells through the tissue. If b2 4ac = 0, then the pde is parabolic (heat). If b2 4ac > 0, then the pde is hyperbolic (wave). This pde has to be. (6.1) ut = ∆u + f is a prototypical example of a parabolic pde.
SOLUTION Chapter 7 parabolic differential equations Studypool
Tumor growth models describe the diffusion of cancer cells through the tissue. If b2 4ac = 0, then the pde is parabolic (heat). (6.1) ut = ∆u + f is a prototypical example of a parabolic pde. If b2 4ac > 0, then the pde is hyperbolic (wave). This pde has to be.
(PDF) Normal Forms For Parabolic Partial Differential Equations
If b2 4ac > 0, then the pde is hyperbolic (wave). (6.1) ut = ∆u + f is a prototypical example of a parabolic pde. This pde has to be. If b2 4ac = 0, then the pde is parabolic (heat). Tumor growth models describe the diffusion of cancer cells through the tissue.
(PDF) Some Stable Difference Approximations to a FourthOrder Parabolic
This pde has to be. If b2 4ac = 0, then the pde is parabolic (heat). (6.1) ut = ∆u + f is a prototypical example of a parabolic pde. Tumor growth models describe the diffusion of cancer cells through the tissue. If b2 4ac > 0, then the pde is hyperbolic (wave).
(PDF) Parameteruniformly convergent numerical scheme for singularly
If b2 4ac = 0, then the pde is parabolic (heat). This pde has to be. If b2 4ac > 0, then the pde is hyperbolic (wave). Tumor growth models describe the diffusion of cancer cells through the tissue. (6.1) ut = ∆u + f is a prototypical example of a parabolic pde.
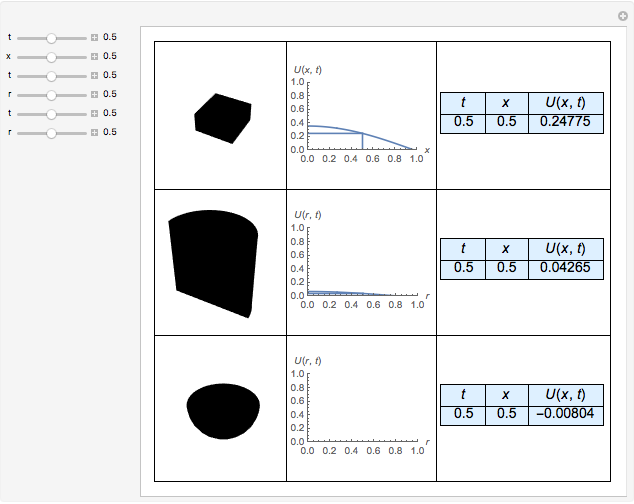
A Parabolic Partial Differential Equation in Three Different Geometries
This pde has to be. If b2 4ac = 0, then the pde is parabolic (heat). Tumor growth models describe the diffusion of cancer cells through the tissue. (6.1) ut = ∆u + f is a prototypical example of a parabolic pde. If b2 4ac > 0, then the pde is hyperbolic (wave).
PPT Parabolic Partial Differential Equations PowerPoint Presentation
(6.1) ut = ∆u + f is a prototypical example of a parabolic pde. Tumor growth models describe the diffusion of cancer cells through the tissue. If b2 4ac > 0, then the pde is hyperbolic (wave). If b2 4ac = 0, then the pde is parabolic (heat). This pde has to be.
(6.1) Ut = ∆U + F Is A Prototypical Example Of A Parabolic Pde.
If b2 4ac > 0, then the pde is hyperbolic (wave). If b2 4ac = 0, then the pde is parabolic (heat). Tumor growth models describe the diffusion of cancer cells through the tissue. This pde has to be.