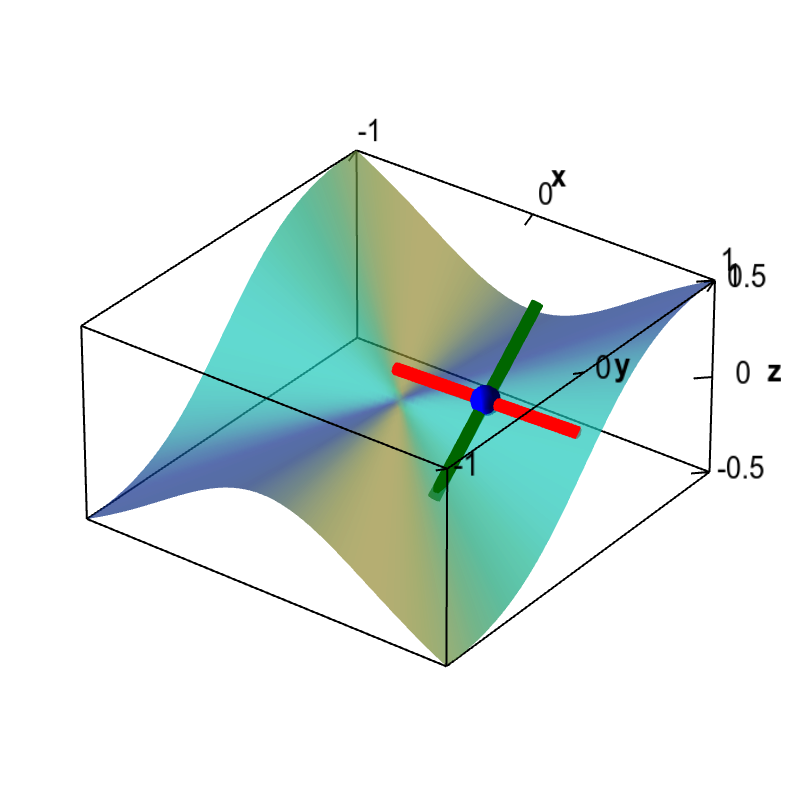
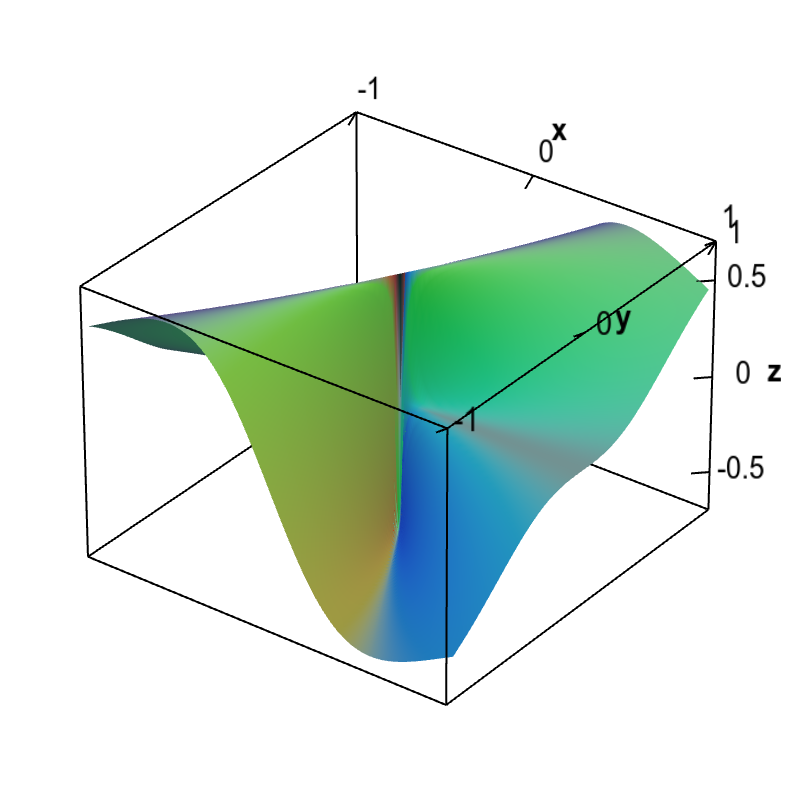
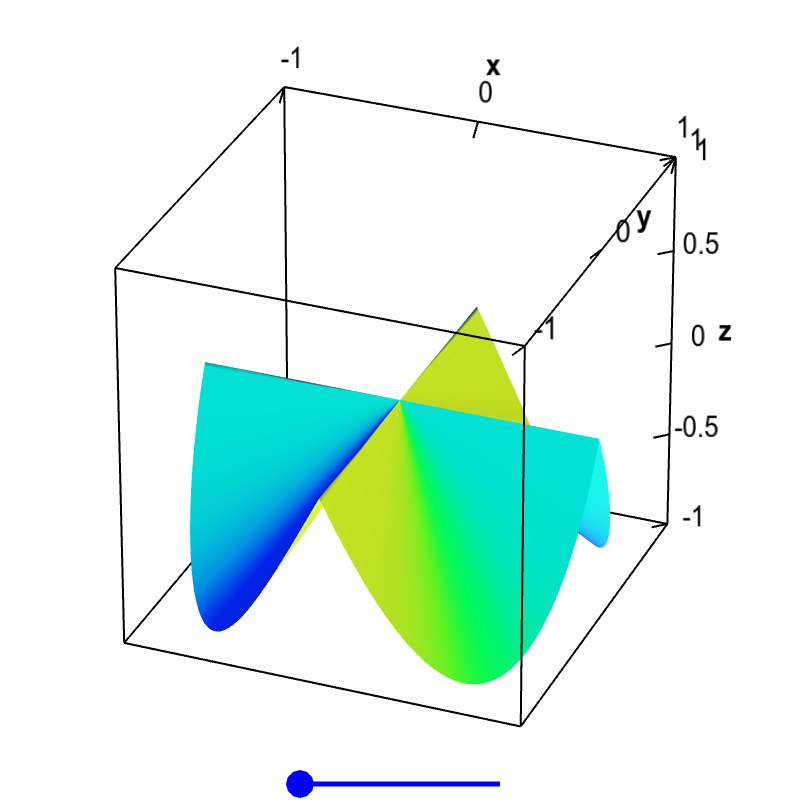Non Differentiable Functions - In the case of functions of one variable it is a function that does not have a. A function that does not have a unique tangent. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. How can we make sense of a delta function that isn't really a function? If you can't find a. So a point where the function is not differentiable is a point where this limit does not exist, that is,. Differentiable functions are ones you can find a derivative (slope) for.
Differentiable functions are ones you can find a derivative (slope) for. A function that does not have a unique tangent. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. So a point where the function is not differentiable is a point where this limit does not exist, that is,. In the case of functions of one variable it is a function that does not have a. How can we make sense of a delta function that isn't really a function? If you can't find a.
So a point where the function is not differentiable is a point where this limit does not exist, that is,. If you can't find a. How can we make sense of a delta function that isn't really a function? A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. A function that does not have a unique tangent. In the case of functions of one variable it is a function that does not have a. Differentiable functions are ones you can find a derivative (slope) for.
Applet Nondifferentiable function with partial derivatives Math Insight
A function that does not have a unique tangent. In the case of functions of one variable it is a function that does not have a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. If you can't find a. Differentiable functions are ones you can find a.
2.7, Non differentiable Functions Math 231 022 JCCC Studocu
A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. How can we make sense of a delta function that isn't really a function? Differentiable functions are ones you can find a derivative (slope) for. In the case of functions of one variable it is a function that does.
Nondifferentiable functions must have discontinuous partial
How can we make sense of a delta function that isn't really a function? In the case of functions of one variable it is a function that does not have a. Differentiable functions are ones you can find a derivative (slope) for. If you can't find a. So a point where the function is not differentiable is a point where.
Differentiable function Wikiwand
Differentiable functions are ones you can find a derivative (slope) for. In the case of functions of one variable it is a function that does not have a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. So a point where the function is not differentiable is a.
Nondifferentiable functions must have discontinuous partial
Differentiable functions are ones you can find a derivative (slope) for. How can we make sense of a delta function that isn't really a function? A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. In the case of functions of one variable it is a function that does.
The figure shows graphs of four useful but nondifferentiable Quizlet
In the case of functions of one variable it is a function that does not have a. How can we make sense of a delta function that isn't really a function? So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which jumps is not differentiable at the.
(PDF) Newton's method for nondifferentiable functions
So a point where the function is not differentiable is a point where this limit does not exist, that is,. How can we make sense of a delta function that isn't really a function? A function that does not have a unique tangent. In the case of functions of one variable it is a function that does not have a..
(PDF) Continuous Nowhere Differentiable Functions (MS Thesis)
If you can't find a. How can we make sense of a delta function that isn't really a function? A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. So a point where the function is not differentiable is a point where this limit does not exist, that is,..
On Correctness of Automatic Differentiation for NonDifferentiable
So a point where the function is not differentiable is a point where this limit does not exist, that is,. If you can't find a. How can we make sense of a delta function that isn't really a function? A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at..
(PDF) Mountain pass theorems for nondifferentiable functions and
So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. If you can't find a. A function that does not have a unique tangent. How can we make sense.
In The Case Of Functions Of One Variable It Is A Function That Does Not Have A.
A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. How can we make sense of a delta function that isn't really a function? If you can't find a. A function that does not have a unique tangent.
Differentiable Functions Are Ones You Can Find A Derivative (Slope) For.
So a point where the function is not differentiable is a point where this limit does not exist, that is,.