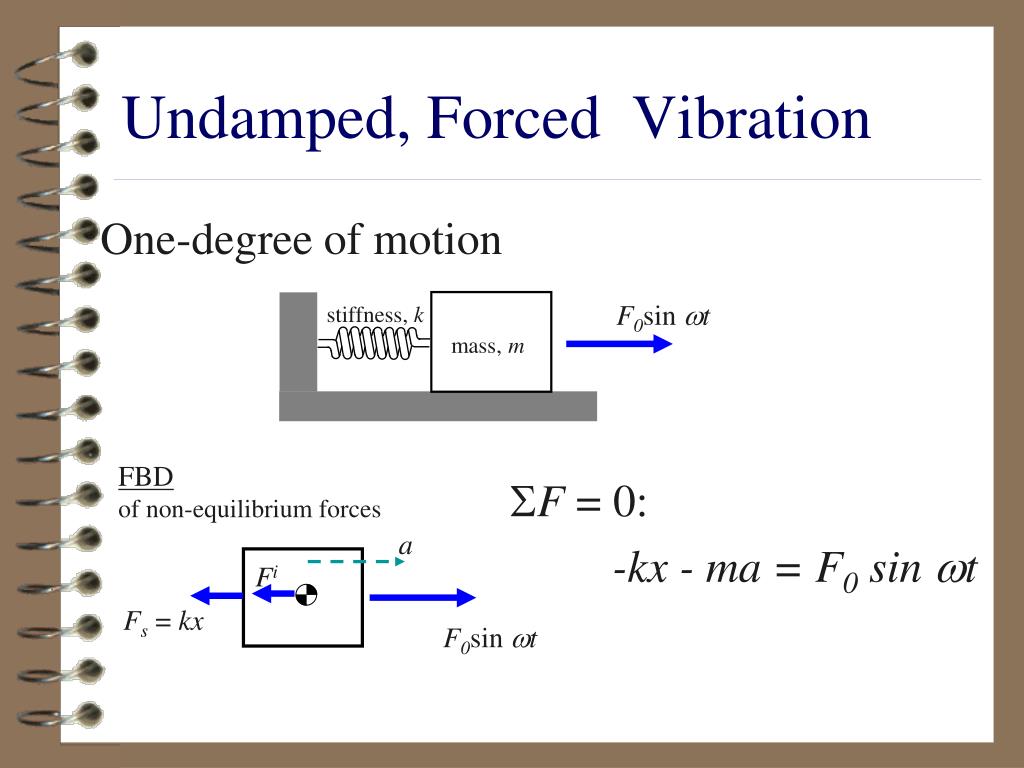
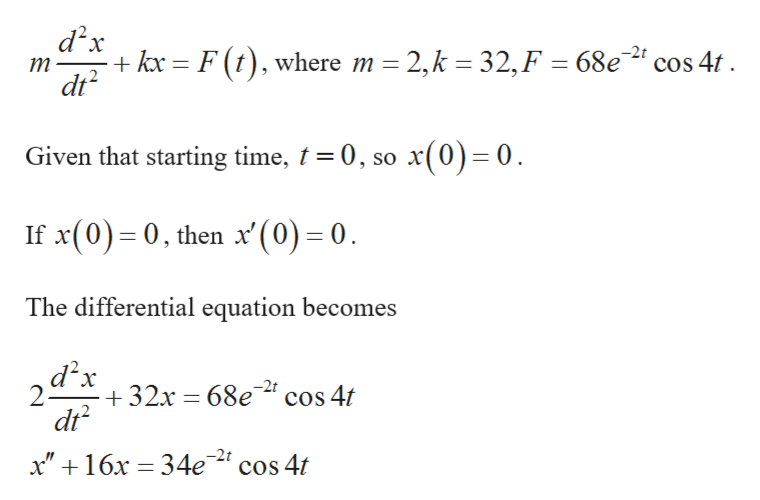Mechanical Vibrations Differential Equations - Simple mechanical vibrations satisfy the following differential equation: Next we are also going to be using the following equations: By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. Mu′′(t) + γu′(t) + ku(t) = fexternal ,. If the forcing function (𝑡) is not equals to zero, eq.
By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. Mu′′(t) + γu′(t) + ku(t) = fexternal ,. Next we are also going to be using the following equations: If the forcing function (𝑡) is not equals to zero, eq. Simple mechanical vibrations satisfy the following differential equation:
Next we are also going to be using the following equations: Simple mechanical vibrations satisfy the following differential equation: By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. Mu′′(t) + γu′(t) + ku(t) = fexternal ,. If the forcing function (𝑡) is not equals to zero, eq.
PPT Mechanical Vibrations PowerPoint Presentation, free download ID
Mu′′(t) + γu′(t) + ku(t) = fexternal ,. Simple mechanical vibrations satisfy the following differential equation: Next we are also going to be using the following equations: By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. If the forcing function (𝑡) is not equals to.
Pauls Online Notes _ Differential Equations Mechanical Vibrations
Next we are also going to be using the following equations: Mu′′(t) + γu′(t) + ku(t) = fexternal ,. By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. If the forcing function (𝑡) is not equals to zero, eq. Simple mechanical vibrations satisfy the following.
PPT Mechanical Vibrations PowerPoint Presentation, free download ID
If the forcing function (𝑡) is not equals to zero, eq. Mu′′(t) + γu′(t) + ku(t) = fexternal ,. By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. Next we are also going to be using the following equations: Simple mechanical vibrations satisfy the following.
Mechanical Engineering Mechanical Vibrations Multi Degree of Freedom
Simple mechanical vibrations satisfy the following differential equation: Next we are also going to be using the following equations: If the forcing function (𝑡) is not equals to zero, eq. Mu′′(t) + γu′(t) + ku(t) = fexternal ,. By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c.
1/3 Mechanical Vibrations — Mnemozine
By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. Simple mechanical vibrations satisfy the following differential equation: Mu′′(t) + γu′(t) + ku(t) = fexternal ,. If the forcing function (𝑡) is not equals to zero, eq. Next we are also going to be using the.
Day 24 MATH241 (Differential Equations) CH 3.7 Mechanical and
Next we are also going to be using the following equations: Mu′′(t) + γu′(t) + ku(t) = fexternal ,. By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. If the forcing function (𝑡) is not equals to zero, eq. Simple mechanical vibrations satisfy the following.
Forced Vibrations Notes 2018 PDF Damping Ordinary Differential
Simple mechanical vibrations satisfy the following differential equation: By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. Mu′′(t) + γu′(t) + ku(t) = fexternal ,. If the forcing function (𝑡) is not equals to zero, eq. Next we are also going to be using the.
SOLVED 'This question is on mechanical vibrations in differential
Simple mechanical vibrations satisfy the following differential equation: Mu′′(t) + γu′(t) + ku(t) = fexternal ,. By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. If the forcing function (𝑡) is not equals to zero, eq. Next we are also going to be using the.
Answered Mechanincal Vibrations (Differential… bartleby
Mu′′(t) + γu′(t) + ku(t) = fexternal ,. Next we are also going to be using the following equations: If the forcing function (𝑡) is not equals to zero, eq. Simple mechanical vibrations satisfy the following differential equation: By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c.
Differential Equations Midterm Examination Mechanical Engineering
If the forcing function (𝑡) is not equals to zero, eq. Mu′′(t) + γu′(t) + ku(t) = fexternal ,. Next we are also going to be using the following equations: By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. Simple mechanical vibrations satisfy the following.
Next We Are Also Going To Be Using The Following Equations:
Mu′′(t) + γu′(t) + ku(t) = fexternal ,. If the forcing function (𝑡) is not equals to zero, eq. By elementary principles we find li′ + ri + q c = e l i ′ + r i + q c = e. Simple mechanical vibrations satisfy the following differential equation: