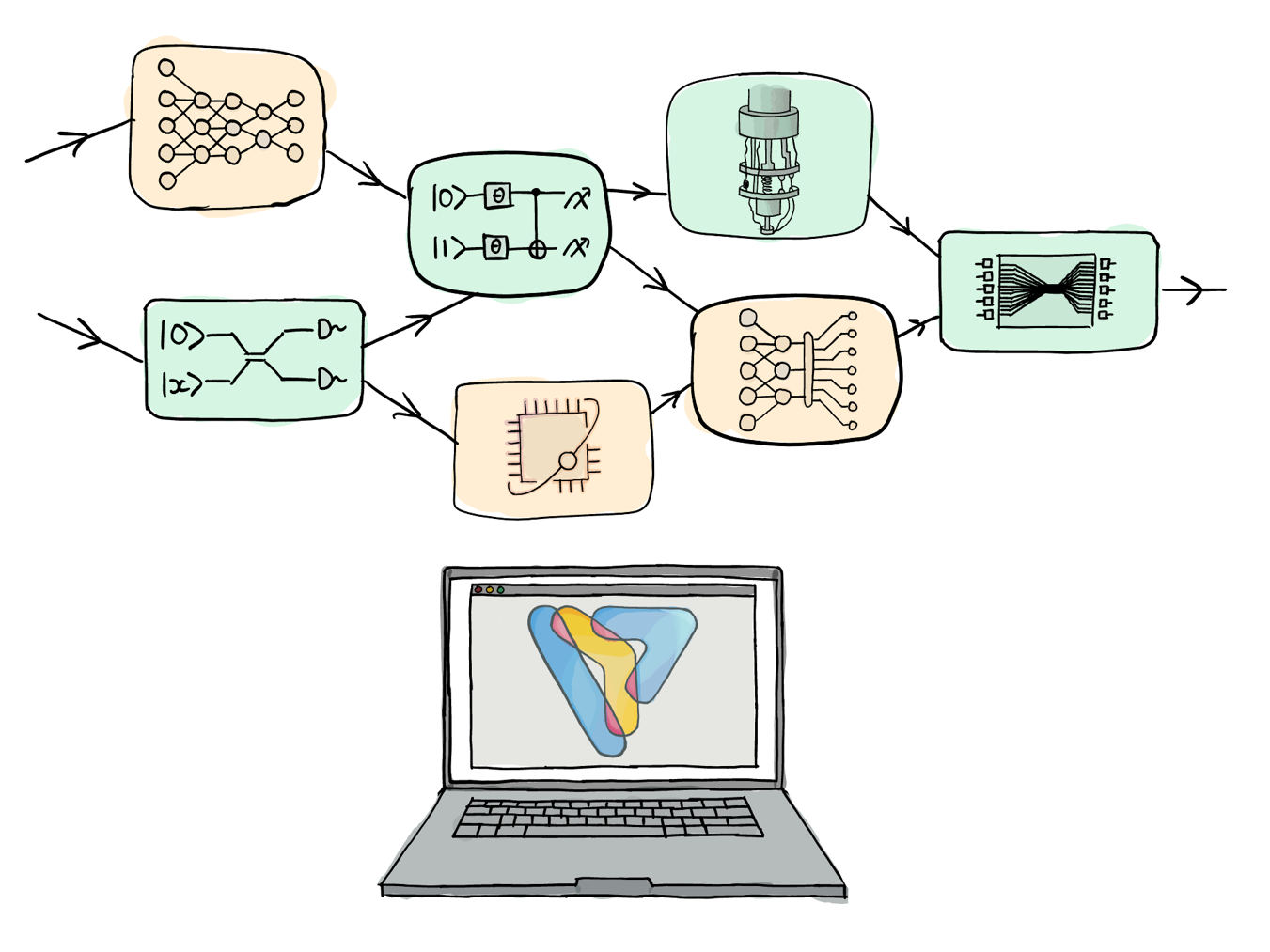
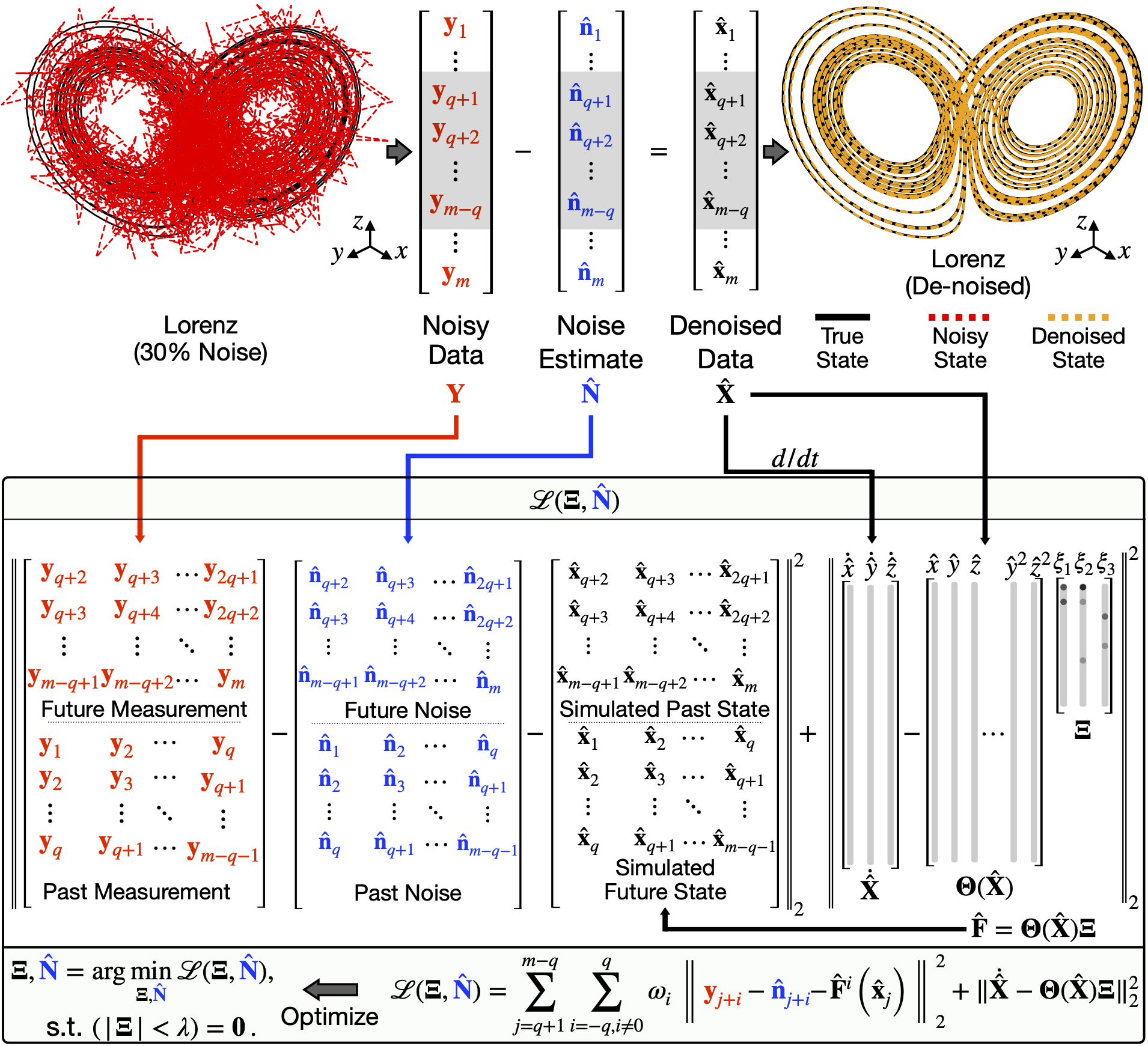
Hypercomplexed-Based Automatic Differentiation - The following tabs contains lecture notes on hypercomplex automatic differentiation. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. From implicit differentiation to probabilistic modeling, jacobians and hessians. In this work, a novel methodology is introduced that uses hypercomplex automatic. Hypercomplex automatic differentiation is a highly accurate numerical.
The following tabs contains lecture notes on hypercomplex automatic differentiation. In this work, a novel methodology is introduced that uses hypercomplex automatic. Hypercomplex automatic differentiation is a highly accurate numerical. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. From implicit differentiation to probabilistic modeling, jacobians and hessians.
Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. From implicit differentiation to probabilistic modeling, jacobians and hessians. The following tabs contains lecture notes on hypercomplex automatic differentiation. In this work, a novel methodology is introduced that uses hypercomplex automatic. Hypercomplex automatic differentiation is a highly accurate numerical.
Sellforte Automatic differentiation, differentiable programming, and
In this work, a novel methodology is introduced that uses hypercomplex automatic. From implicit differentiation to probabilistic modeling, jacobians and hessians. Hypercomplex automatic differentiation is a highly accurate numerical. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. The following tabs contains lecture notes on hypercomplex automatic differentiation.
PennyLane Automatic differentiation of hybrid quantumclassical
In this work, a novel methodology is introduced that uses hypercomplex automatic. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. The following tabs contains lecture notes on hypercomplex automatic differentiation. Hypercomplex automatic differentiation is a highly accurate numerical. From implicit differentiation to probabilistic modeling, jacobians and hessians.
Automatic Differentiation to Simultaneously Identify Dynamics
In this work, a novel methodology is introduced that uses hypercomplex automatic. The following tabs contains lecture notes on hypercomplex automatic differentiation. From implicit differentiation to probabilistic modeling, jacobians and hessians. Hypercomplex automatic differentiation is a highly accurate numerical. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode.
Automatic differentiation Semantic Scholar
Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. Hypercomplex automatic differentiation is a highly accurate numerical. The following tabs contains lecture notes on hypercomplex automatic differentiation. From implicit differentiation to probabilistic modeling, jacobians and hessians. In this work, a novel methodology is introduced that uses hypercomplex automatic.
A Functional Tour of Automatic Differentiation InfoQ
From implicit differentiation to probabilistic modeling, jacobians and hessians. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. Hypercomplex automatic differentiation is a highly accurate numerical. The following tabs contains lecture notes on hypercomplex automatic differentiation. In this work, a novel methodology is introduced that uses hypercomplex automatic.
Softwarebased Automatic Differentiation is Flawed Paper and Code
The following tabs contains lecture notes on hypercomplex automatic differentiation. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. In this work, a novel methodology is introduced that uses hypercomplex automatic. From implicit differentiation to probabilistic modeling, jacobians and hessians. Hypercomplex automatic differentiation is a highly accurate numerical.
machine learning Automatic differentiation for incrementally updated
The following tabs contains lecture notes on hypercomplex automatic differentiation. In this work, a novel methodology is introduced that uses hypercomplex automatic. Hypercomplex automatic differentiation is a highly accurate numerical. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. From implicit differentiation to probabilistic modeling, jacobians and hessians.
Softwarebased Automatic Differentiation is Flawed Paper and Code
Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. The following tabs contains lecture notes on hypercomplex automatic differentiation. In this work, a novel methodology is introduced that uses hypercomplex automatic. From implicit differentiation to probabilistic modeling, jacobians and hessians. Hypercomplex automatic differentiation is a highly accurate numerical.
Softwarebased Automatic Differentiation is Flawed Paper and Code
Hypercomplex automatic differentiation is a highly accurate numerical. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. From implicit differentiation to probabilistic modeling, jacobians and hessians. The following tabs contains lecture notes on hypercomplex automatic differentiation. In this work, a novel methodology is introduced that uses hypercomplex automatic.
(PDF) Beyond automatic differentiation
In this work, a novel methodology is introduced that uses hypercomplex automatic. Automatic differentiation can be performed in forward mode, reverse mode, or mixed mode. From implicit differentiation to probabilistic modeling, jacobians and hessians. Hypercomplex automatic differentiation is a highly accurate numerical. The following tabs contains lecture notes on hypercomplex automatic differentiation.
Automatic Differentiation Can Be Performed In Forward Mode, Reverse Mode, Or Mixed Mode.
Hypercomplex automatic differentiation is a highly accurate numerical. The following tabs contains lecture notes on hypercomplex automatic differentiation. In this work, a novel methodology is introduced that uses hypercomplex automatic. From implicit differentiation to probabilistic modeling, jacobians and hessians.