Gateaux Differentiable - If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). Gˆateaux derivative is a generalization of the concept of. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional.
In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). Gˆateaux derivative is a generalization of the concept of.
Gˆateaux derivative is a generalization of the concept of. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0).
Fresh Fruit Gateaux Solstice Foods
If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. Gˆateaux derivative is a generalization of the concept.
(PDF) Gâteaux differentiable norms in MusiełakOrlicz spaces
If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). Gˆateaux derivative is a generalization of the concept of. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of.
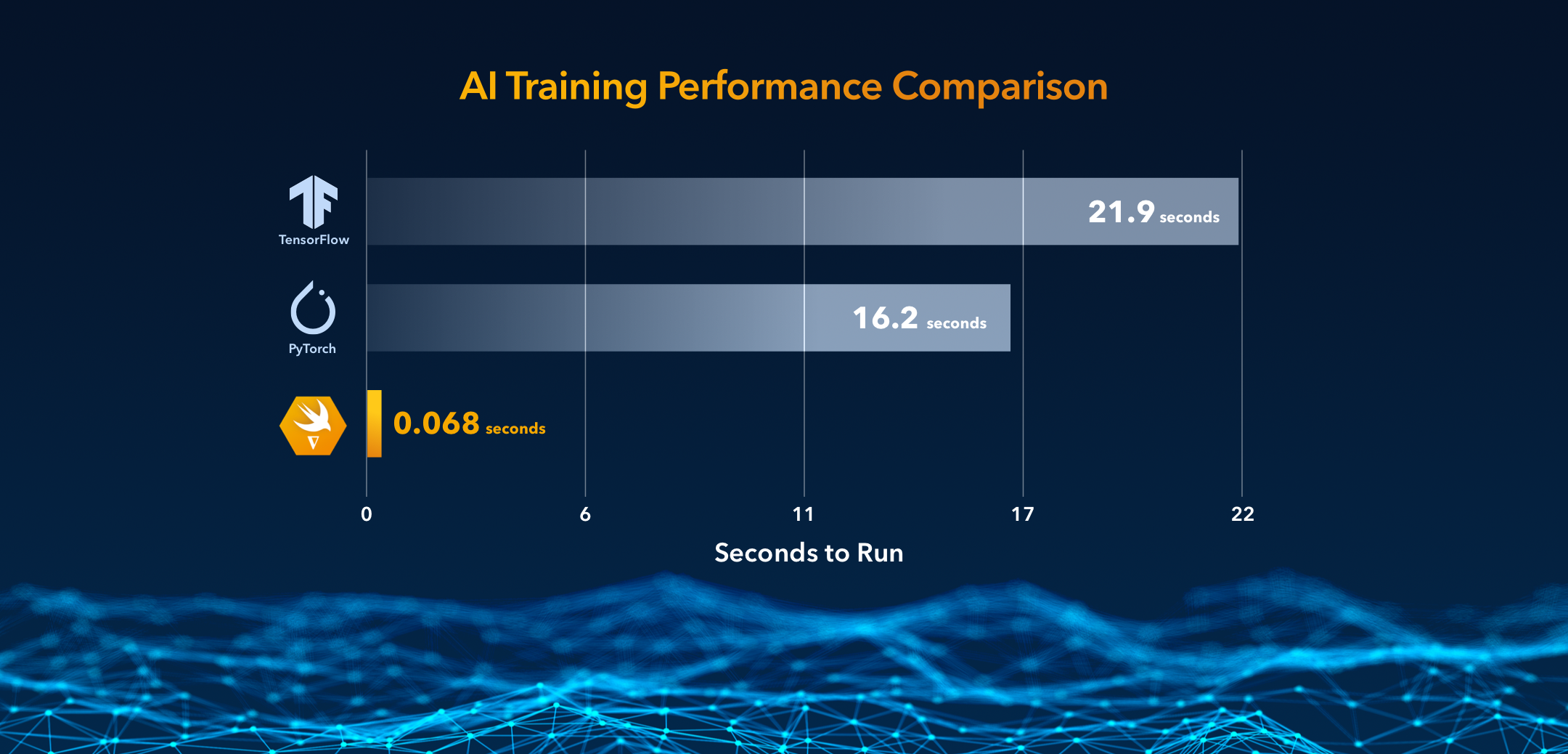
Differentiable Swift
If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. Gˆateaux derivative is a generalization of the concept of. In mathematics, the fr ́echet derivative is a derivative define on banach.
SOLVEDLet X be a Banach space with a Gâteaux differentiable norm. Let
In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. Gˆateaux derivative is a generalization of the concept of. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) =.
Gateaux Lamis Dania Delesyo
In mathematics, the fr ́echet derivative is a derivative define on banach spaces. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. Gˆateaux derivative is a generalization of the concept of. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) =.
(PDF) Construction of pathological Gâteaux differentiable functions
In mathematics, the fr ́echet derivative is a derivative define on banach spaces. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). Gˆateaux derivative is a generalization of the concept.
(PDF) Distributional Volterra series, and analysis of sequentially
In mathematics, the fr ́echet derivative is a derivative define on banach spaces. Gˆateaux derivative is a generalization of the concept of. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) =.
FileTypes of dessert gateaux.jpeg Wikimedia Commons
If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). Gˆateaux derivative is a generalization of the concept of. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. In mathematics, the fr ́echet derivative is a derivative define on banach.
Differentiable Font download free
In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. Gˆateaux derivative is a generalization of the concept.
lesgateauxdegrandmere les recettes gourmandes des petits bonheurs
In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional. In mathematics, the fr ́echet derivative is a derivative define on banach spaces. If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). Gˆateaux derivative is a generalization of the concept.
Gˆateaux Derivative Is A Generalization Of The Concept Of.
If $\phi$ is continuous at $x_0$ and ∂ϕ(x0) contains a singleton element, then ϕ is gâteaux differentiable at x0 and ϕ(x0) = ∂ϕ(x0). In mathematics, the fr ́echet derivative is a derivative define on banach spaces. In mathematics, the gâteaux differential or gâteaux derivative is a generalization of the concept of directional.