Elliptic Partial Differential Equations - A solution to this equation is u(x; Praise for the first edition: Differential operator of one of the two forms: Lu= xn i,j=1 a ij(x)∂ iju(a non. Thus, the laplace equation is elliptic. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Elliptic partial differential equations by qing. Primarily the dirichlet problem for various types of elliptic equations. This could model the temperature distribution on a square floor.
Thus, the laplace equation is elliptic. Elliptic partial differential equations by qing. Differential operator of one of the two forms: This could model the temperature distribution on a square floor. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Praise for the first edition: A solution to this equation is u(x; Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Lu= xn i,j=1 a ij(x)∂ iju(a non. Primarily the dirichlet problem for various types of elliptic equations.
Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. This could model the temperature distribution on a square floor. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Elliptic partial differential equations by qing. Primarily the dirichlet problem for various types of elliptic equations. Praise for the first edition: Differential operator of one of the two forms: Thus, the laplace equation is elliptic. Lu= xn i,j=1 a ij(x)∂ iju(a non. A solution to this equation is u(x;
[Solved] Problem 1. Second order Partial differential equations (PDEs
Primarily the dirichlet problem for various types of elliptic equations. Lu= xn i,j=1 a ij(x)∂ iju(a non. Thus, the laplace equation is elliptic. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Praise for the first edition:
Lecture 7_elliptic partial differential equation PDF Equations
Praise for the first edition: Thus, the laplace equation is elliptic. A solution to this equation is u(x; Elliptic partial differential equations by qing. This could model the temperature distribution on a square floor.
Solved Consider the elliptic partial differential equation
Primarily the dirichlet problem for various types of elliptic equations. This could model the temperature distribution on a square floor. A solution to this equation is u(x; Differential operator of one of the two forms: Thus, the laplace equation is elliptic.
(PDF) Elliptic Partial Differential Equations Qualitative
This could model the temperature distribution on a square floor. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Lu= xn i,j=1 a ij(x)∂ iju(a non. A solution to this equation is u(x; Differential operator of one of the two forms:
PPT PARTIAL DIFFERENTIAL EQUATIONS PowerPoint Presentation ID2511480
Elliptic partial differential equations by qing. Primarily the dirichlet problem for various types of elliptic equations. Thus, the laplace equation is elliptic. This could model the temperature distribution on a square floor. Lu= xn i,j=1 a ij(x)∂ iju(a non.
(PDF) The numerical solution of elliptic partial differential equations
Elliptic partial differential equations by qing. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. A solution to this equation is u(x; Lu= xn i,j=1 a ij(x)∂ iju(a non. Primarily the dirichlet problem for various types of elliptic equations.
(PDF) Numerical Solutions of Elliptic Partial Differential Equations by
Differential operator of one of the two forms: Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Lu= xn i,j=1 a ij(x)∂ iju(a non. Elliptic partial differential equations by qing. Primarily the dirichlet problem for various types of elliptic equations.
Solved Solve the elliptic partial differential equation
This could model the temperature distribution on a square floor. Lu= xn i,j=1 a ij(x)∂ iju(a non. Primarily the dirichlet problem for various types of elliptic equations. Differential operator of one of the two forms: A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients.
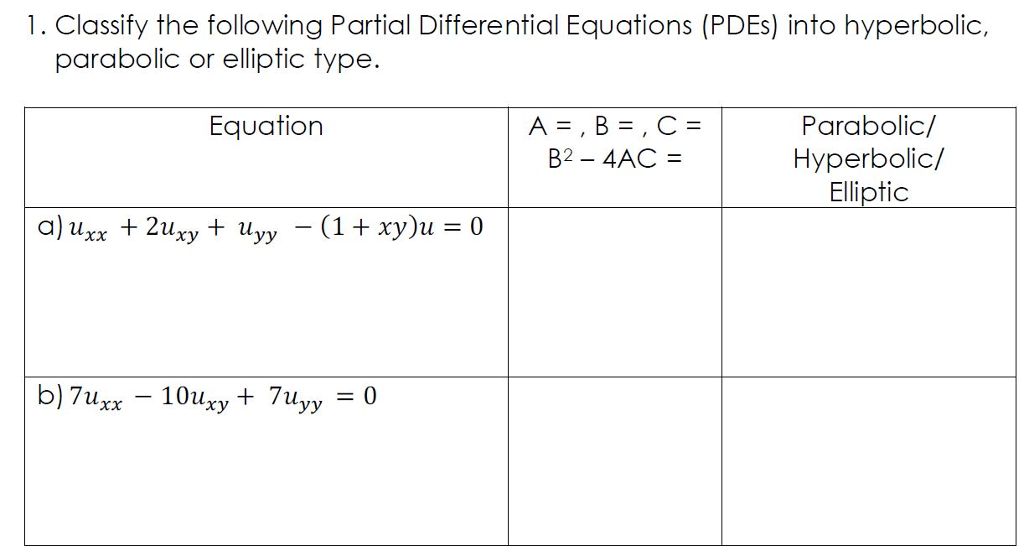
Solved 1. Classify the following Partial Differential
Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. This could model the temperature distribution on a square floor. Primarily the dirichlet problem for various types of elliptic equations. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Thus, the laplace equation is elliptic.
PPT Elliptic Partial Differential Equations Introduction PowerPoint
Thus, the laplace equation is elliptic. A solution to this equation is u(x; Praise for the first edition: A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Differential operator of one of the two forms:
Differential Operator Of One Of The Two Forms:
Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Praise for the first edition: Thus, the laplace equation is elliptic. This could model the temperature distribution on a square floor.
A Course On The Method Of Pseudodifferential Operators For Elliptic Pdes With Constant And Variable Coefficients.
A solution to this equation is u(x; Elliptic partial differential equations by qing. Lu= xn i,j=1 a ij(x)∂ iju(a non. Primarily the dirichlet problem for various types of elliptic equations.