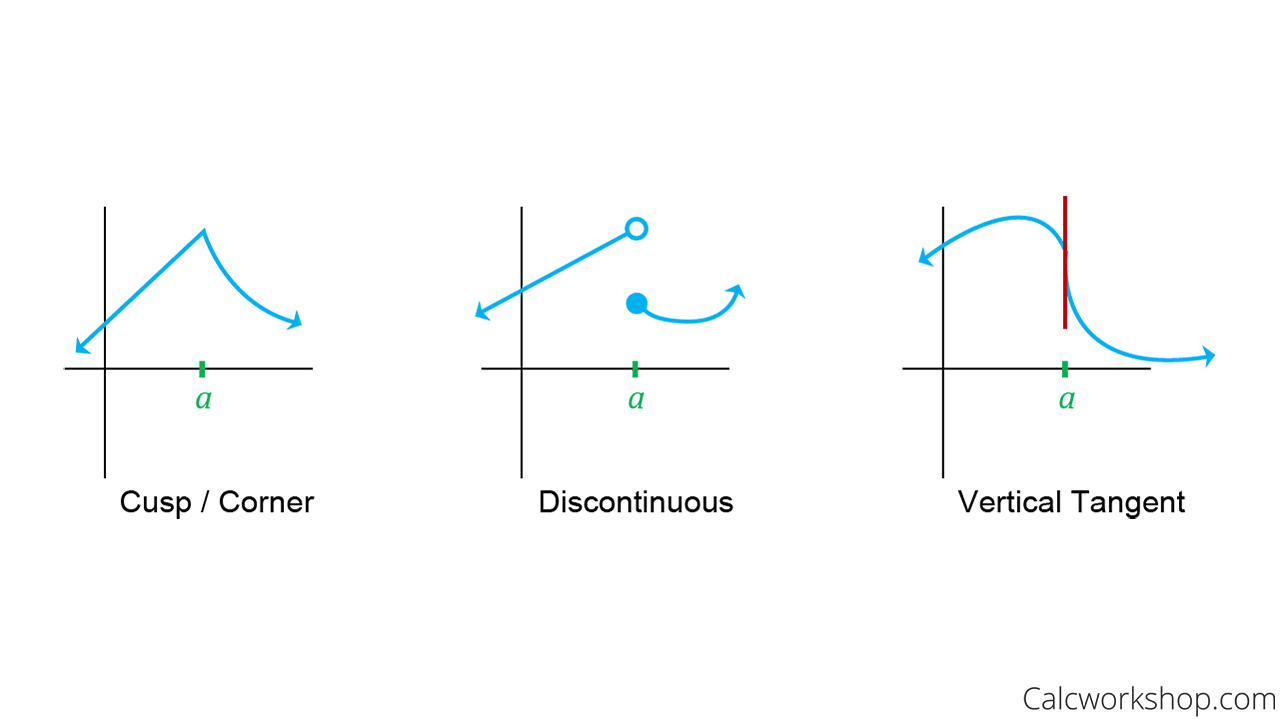
Does Continuity Imply Differentiability - Differentiability requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x. Relation between continuity and differentiability: The web page also explains the. Differentiability is a stronger condition than continuity. Continuity refers to a definition of the concept of a function that varies without. In other words, if a function can be differentiated at a point, it is. Learn why any differentiable function is automatically continuous, and see the proof and examples. Continuity requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x − y → 0 x − y → 0.
Differentiability is a stronger condition than continuity. Relation between continuity and differentiability: The web page also explains the. Continuity requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x − y → 0 x − y → 0. Continuity refers to a definition of the concept of a function that varies without. Learn why any differentiable function is automatically continuous, and see the proof and examples. Differentiability requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x. In other words, if a function can be differentiated at a point, it is.
Relation between continuity and differentiability: In other words, if a function can be differentiated at a point, it is. Learn why any differentiable function is automatically continuous, and see the proof and examples. Continuity requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x − y → 0 x − y → 0. Continuity refers to a definition of the concept of a function that varies without. Differentiability is a stronger condition than continuity. Differentiability requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x. The web page also explains the.
Continuity and Differentiability (Fully Explained w/ Examples!)
The web page also explains the. Continuity refers to a definition of the concept of a function that varies without. Differentiability is a stronger condition than continuity. Differentiability requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x. Learn why any differentiable function is automatically continuous, and see the proof and examples.
calculus What does differentiability imply in this proof
Relation between continuity and differentiability: Differentiability is a stronger condition than continuity. Continuity refers to a definition of the concept of a function that varies without. The web page also explains the. Learn why any differentiable function is automatically continuous, and see the proof and examples.
derivatives Differentiability Implies Continuity (Multivariable
In other words, if a function can be differentiated at a point, it is. Relation between continuity and differentiability: Differentiability requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x. Differentiability is a stronger condition than continuity. Learn why any differentiable function is automatically continuous, and see the proof and examples.
derivatives Differentiability Implies Continuity (Multivariable
Relation between continuity and differentiability: Differentiability is a stronger condition than continuity. The web page also explains the. In other words, if a function can be differentiated at a point, it is. Continuity refers to a definition of the concept of a function that varies without.
Which of the following is true? (a) differentiability does not imply
Continuity refers to a definition of the concept of a function that varies without. The web page also explains the. Differentiability is a stronger condition than continuity. Relation between continuity and differentiability: Continuity requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x − y → 0 x − y → 0.
Unit 2.2 Connecting Differentiability and Continuity (Notes
Continuity requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x − y → 0 x − y → 0. In other words, if a function can be differentiated at a point, it is. Differentiability is a stronger condition than continuity. Relation between continuity and differentiability: Continuity refers to a definition of the concept.
Which of the following is true? (a) differentiability does not imply
Relation between continuity and differentiability: Differentiability is a stronger condition than continuity. Learn why any differentiable function is automatically continuous, and see the proof and examples. In other words, if a function can be differentiated at a point, it is. Continuity requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x − y →.
Continuity & Differentiability
Differentiability is a stronger condition than continuity. In other words, if a function can be differentiated at a point, it is. Continuity requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x − y → 0 x − y → 0. The web page also explains the. Differentiability requires that f(x) − f(y) →.
Solved Does continuity imply differentiability? Why or why
The web page also explains the. Learn why any differentiable function is automatically continuous, and see the proof and examples. Differentiability requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x. Relation between continuity and differentiability: Continuity requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x −.
Which of the following is true? (a) differentiability does not imply
In other words, if a function can be differentiated at a point, it is. Continuity requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x − y → 0 x − y → 0. Differentiability is a stronger condition than continuity. The web page also explains the. Differentiability requires that f(x) − f(y) →.
Continuity Requires That F(X) − F(Y) → 0 F (X) − F (Y) → 0 As X − Y → 0 X − Y → 0.
Learn why any differentiable function is automatically continuous, and see the proof and examples. Differentiability is a stronger condition than continuity. Relation between continuity and differentiability: In other words, if a function can be differentiated at a point, it is.
Continuity Refers To A Definition Of The Concept Of A Function That Varies Without.
Differentiability requires that f(x) − f(y) → 0 f (x) − f (y) → 0 as x. The web page also explains the.