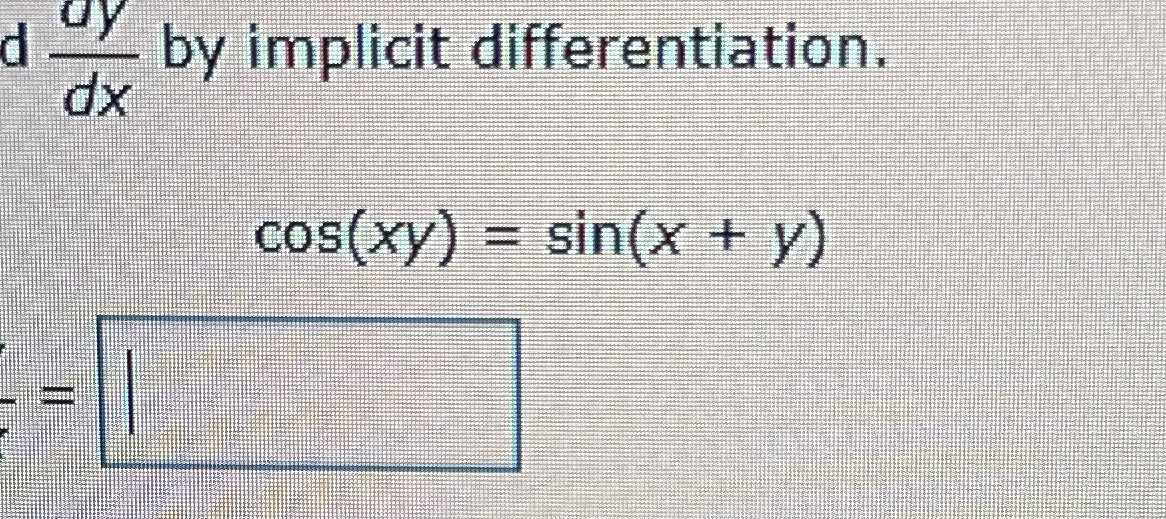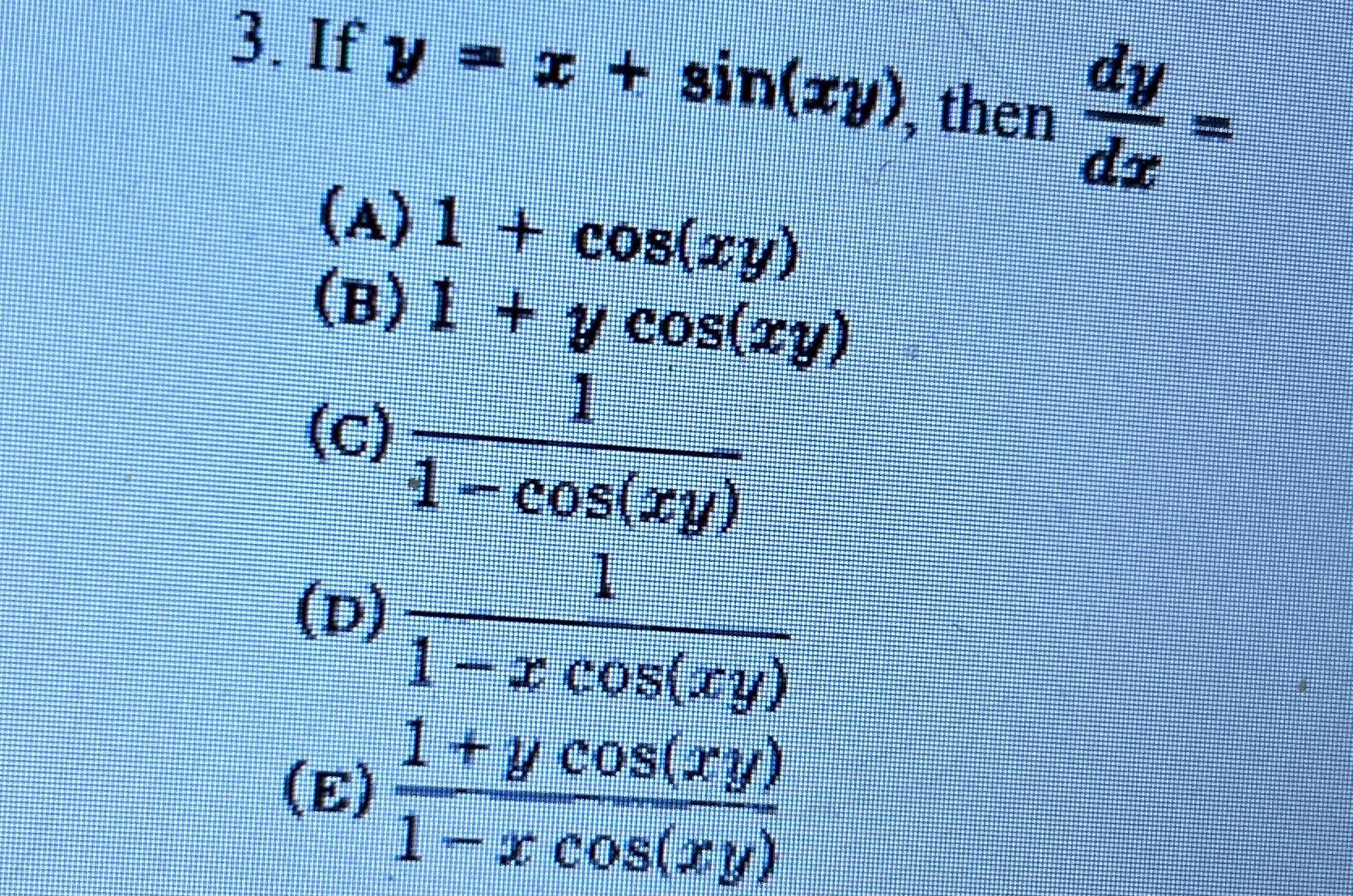Differentiation Of Cos Xy - What is the derivative of cos(xy)? Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more Replace y' y ′ with dy dx d y d x. D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the.
D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: What is the derivative of cos(xy)? Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. Replace y' y ′ with dy dx d y d x. The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x).
Replace y' y ′ with dy dx d y d x. What is the derivative of cos(xy)? D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change.
Solved Given the following differential equation (cos(xy) +
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then.
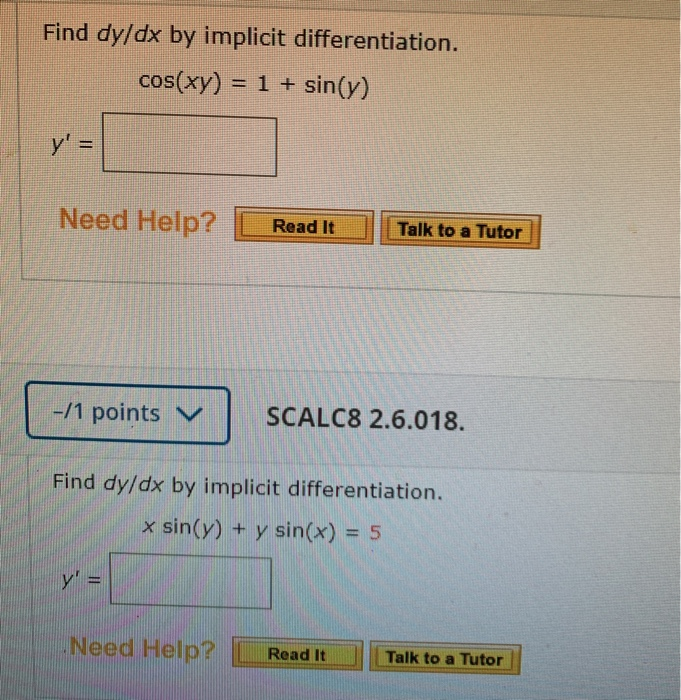
Solved Find dy/dx by implicit differentiation. cos (xy)=sin (x+y) dy
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change..
Solved Use implicit differentiation to find dy/dx. Cos xy +
What is the derivative of cos(xy)? D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x).
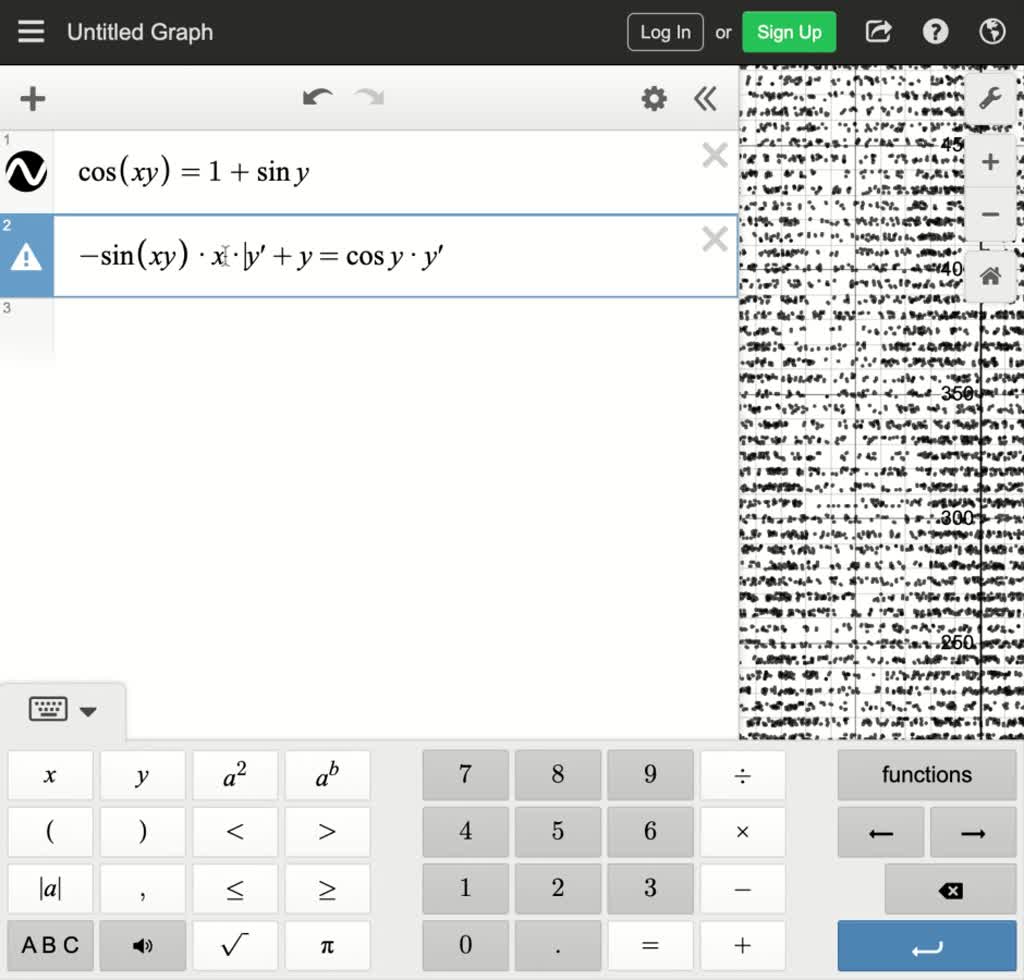
SOLVED Find dy/dx by implicit differentiation. cos(xy) = 1 + siny
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change..
Solved ddydx by implicit differentiation.cos(xy)=sin(x+y)
Replace y' y ′ with dy dx d y d x. What is the derivative of cos(xy)? Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n}.
[Solved] Find dy / dx by implicit differentiation. cos( xy ) = 1 + sin
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. Replace y' y ′ with dy dx d y d x. The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change. D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: D dx.
Solved Find dy/dx by implicit differentiation. cos(xy) = 1 +
D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). What is the derivative of cos(xy)? Free math problem.
Solved Given the following differential equation ( cos(xy?)
What is the derivative of cos(xy)? D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. Replace y' y ′ with dy dx d y d x. \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more
[Solved] Find dy / dx by implicit differentiation. cos( xy ) = 1 + sin
D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: \int e^x\cos (x)dx \int_{0}^{\pi}\sin(x)dx \sum_{n=0}^{\infty}\frac{3}{2^n} show more Replace y' y ′ with dy dx d y d x. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics. The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function,.
Solved If y=x+sin(xy), then
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). What is the derivative of cos(xy)? D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. D dx cos(xy) = −(y.
\Int E^x\Cos (X)Dx \Int_{0}^{\Pi}\Sin(X)Dx \Sum_{N=0}^{\Infty}\Frac{3}{2^N} Show More
Differentiate using the chain rule, which states that d dx [f (g(x))] d d x [f (g (x))] is f '(g(x))g'(x) f ′ (g (x)) g ′ (x) where f (x) = cos(x) f (x) = cos (x). D dx cos(xy) = −(y + x dy dx)sin(xy) use the chain rule: D dx cos(xy) = −sin(xy) ⋅ d dx (xy) then the. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics.
The Differentiation Of Trigonometric Functions Is The Mathematical Process Of Finding The Derivative Of A Trigonometric Function, Or Its Rate Of Change.
What is the derivative of cos(xy)? Replace y' y ′ with dy dx d y d x.