Differentiation Of Absolute Function - Let $\size x$ be the absolute value of $x$ for real $x$. What is the derivative of an absolute value? The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. Since an absolute value function is represented by the graph of two “linear” equations coming together to form a “v” the derivative is a. D dx |u| = u |u| ⋅ du dx. The absolute value function | x | is defined. Y' = 2(x −2) 2√(x − 2)2 → power rule. To understand the derivative of the absolute value function | x |, let’s break it down step by step. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$.
To understand the derivative of the absolute value function | x |, let’s break it down step by step. D dx |u| = u |u| ⋅ du dx. Since an absolute value function is represented by the graph of two “linear” equations coming together to form a “v” the derivative is a. What is the derivative of an absolute value? The absolute value function | x | is defined. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Y' = 2(x −2) 2√(x − 2)2 → power rule. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. Let $\size x$ be the absolute value of $x$ for real $x$.
$\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. The absolute value function | x | is defined. D dx |u| = u |u| ⋅ du dx. What is the derivative of an absolute value? Since an absolute value function is represented by the graph of two “linear” equations coming together to form a “v” the derivative is a. Let $\size x$ be the absolute value of $x$ for real $x$. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. To understand the derivative of the absolute value function | x |, let’s break it down step by step. Y' = 2(x −2) 2√(x − 2)2 → power rule.
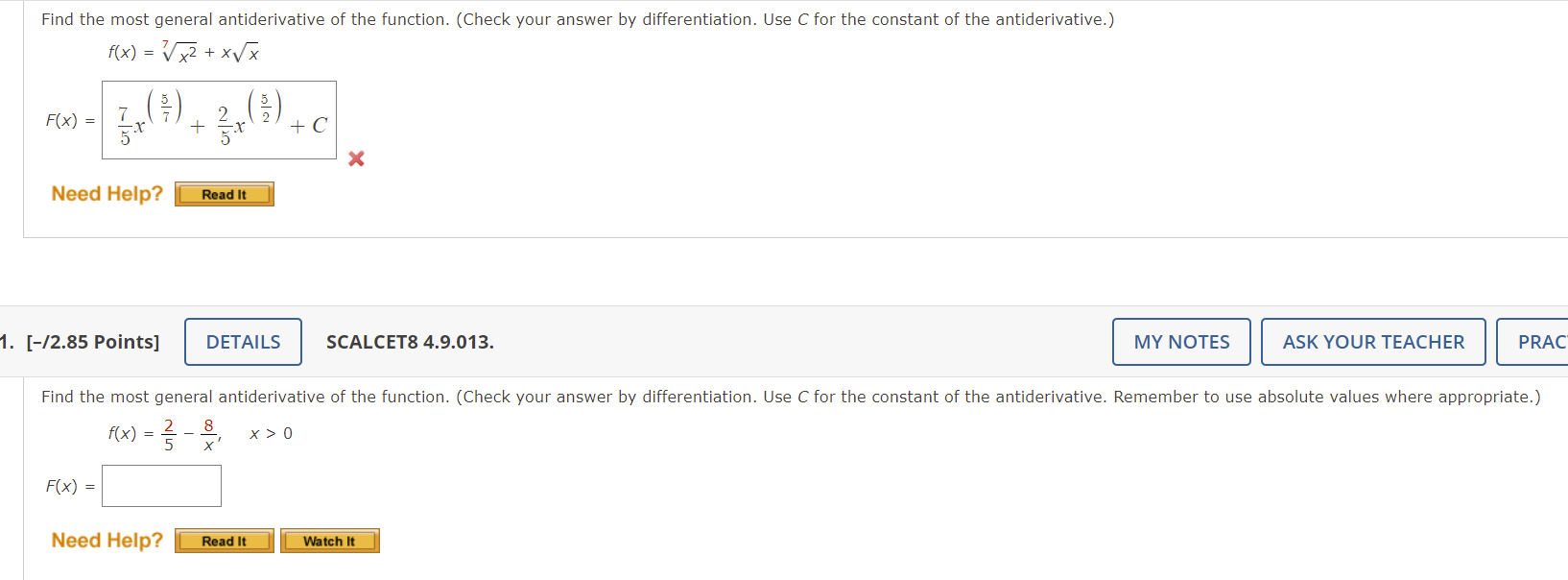
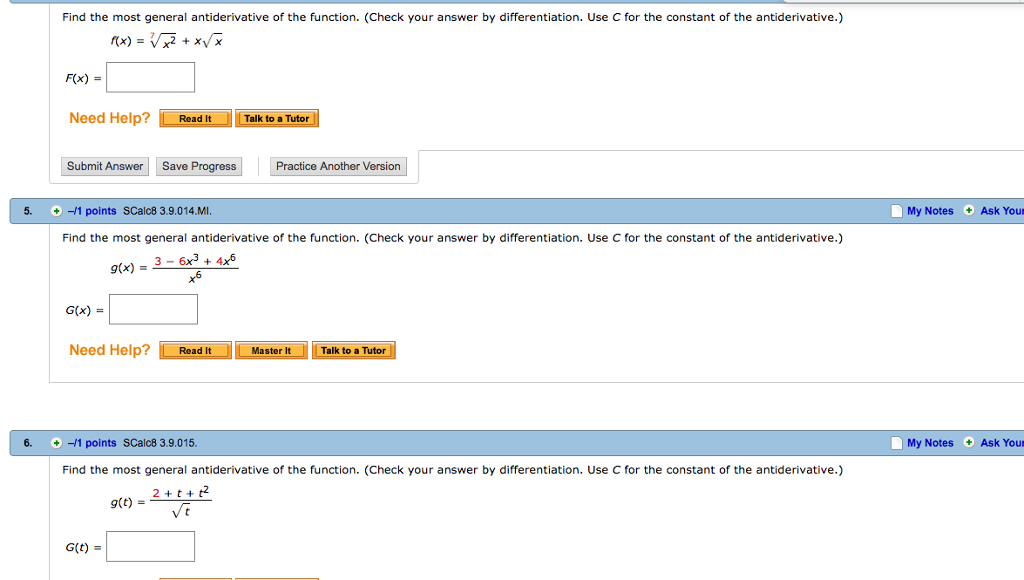
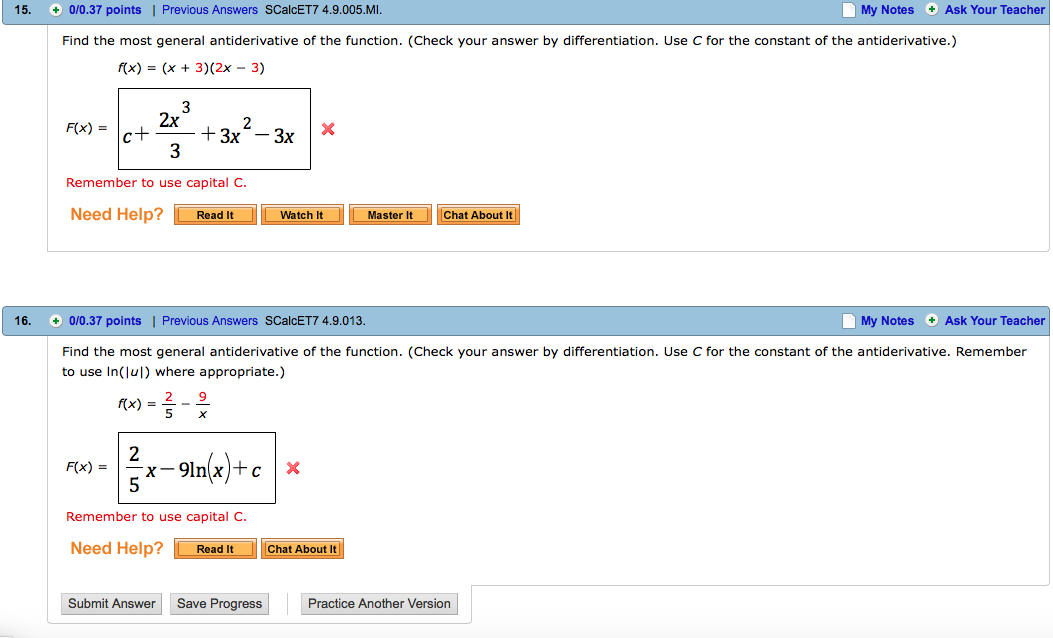
Solved Find the most general antiderivative of the function.
The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. To understand the derivative of the absolute value function | x |, let’s break it down step by step. The absolute value function | x | is defined. D dx |u| = u |u| ⋅ du dx..
1 Absolute Function and Graph It PDF
$\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Y' = 2(x −2) 2√(x − 2)2 → power rule. Since an absolute value function is represented by the graph of two “linear” equations coming together to form a “v” the derivative is a. D dx |u| = u |u| ⋅ du dx. The derivative.
Finding the Derivative of Absolute Value Overview & Examples Video
What is the derivative of an absolute value? $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. D dx |u| = u |u| ⋅ du dx. Since an absolute value function is represented by the graph of two “linear” equations coming together to form a “v” the derivative is a. The absolute value function.
Download Example Of Absolute Function ClipartKey
$\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Since an absolute value function is represented by the graph of two “linear” equations coming together to form a “v” the derivative is a. To understand the derivative of the absolute value function | x |, let’s break it down step by step. D dx.
Differentiate Absolute Value Function
The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. Since an absolute value function is represented by the graph of two “linear” equations coming together to form a “v” the derivative is a. The absolute value function | x | is defined. Let $\size x$ be.
Solved Find the most general antiderivative of the function
To understand the derivative of the absolute value function | x |, let’s break it down step by step. Let $\size x$ be the absolute value of $x$ for real $x$. The absolute value function | x | is defined. Since an absolute value function is represented by the graph of two “linear” equations coming together to form a “v”.
Solved Find the most general antiderivative of the function.
Y' = 2(x −2) 2√(x − 2)2 → power rule. The absolute value function | x | is defined. D dx |u| = u |u| ⋅ du dx. What is the derivative of an absolute value? Since an absolute value function is represented by the graph of two “linear” equations coming together to form a “v” the derivative is a.
Differentiate Absolute Value Function
Let $\size x$ be the absolute value of $x$ for real $x$. What is the derivative of an absolute value? The absolute value function | x | is defined. Y' = 2(x −2) 2√(x − 2)2 → power rule. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$.
Absolute Value Function Khan Academy at Lemuel McLaughlin blog
The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. What is the derivative of an absolute value? Y' = 2(x −2) 2√(x − 2)2 → power rule. Let $\size x$ be the absolute value of $x$ for real $x$. Since an absolute value function is represented.
Differentiate Absolute Value Function
To understand the derivative of the absolute value function | x |, let’s break it down step by step. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Y' = 2(x.
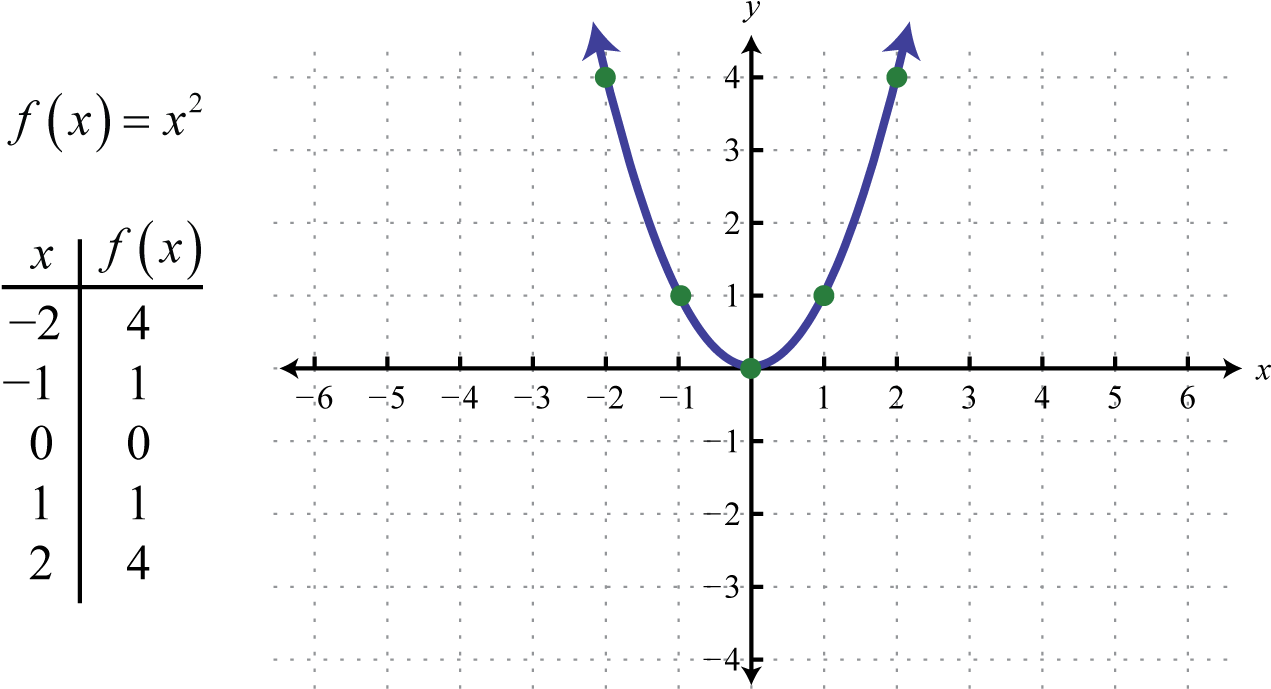
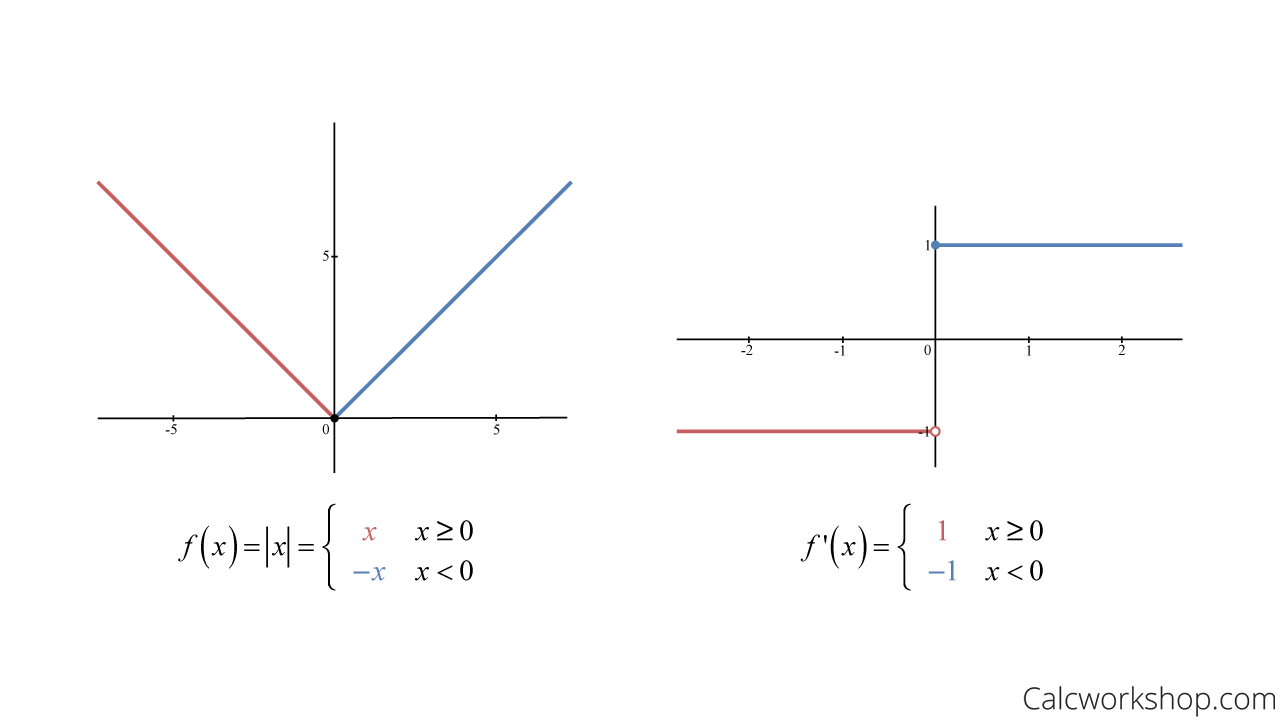
Since An Absolute Value Function Is Represented By The Graph Of Two “Linear” Equations Coming Together To Form A “V” The Derivative Is A.
The absolute value function | x | is defined. To understand the derivative of the absolute value function | x |, let’s break it down step by step. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Let $\size x$ be the absolute value of $x$ for real $x$.
What Is The Derivative Of An Absolute Value?
Y' = 2(x −2) 2√(x − 2)2 → power rule. D dx |u| = u |u| ⋅ du dx. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point.