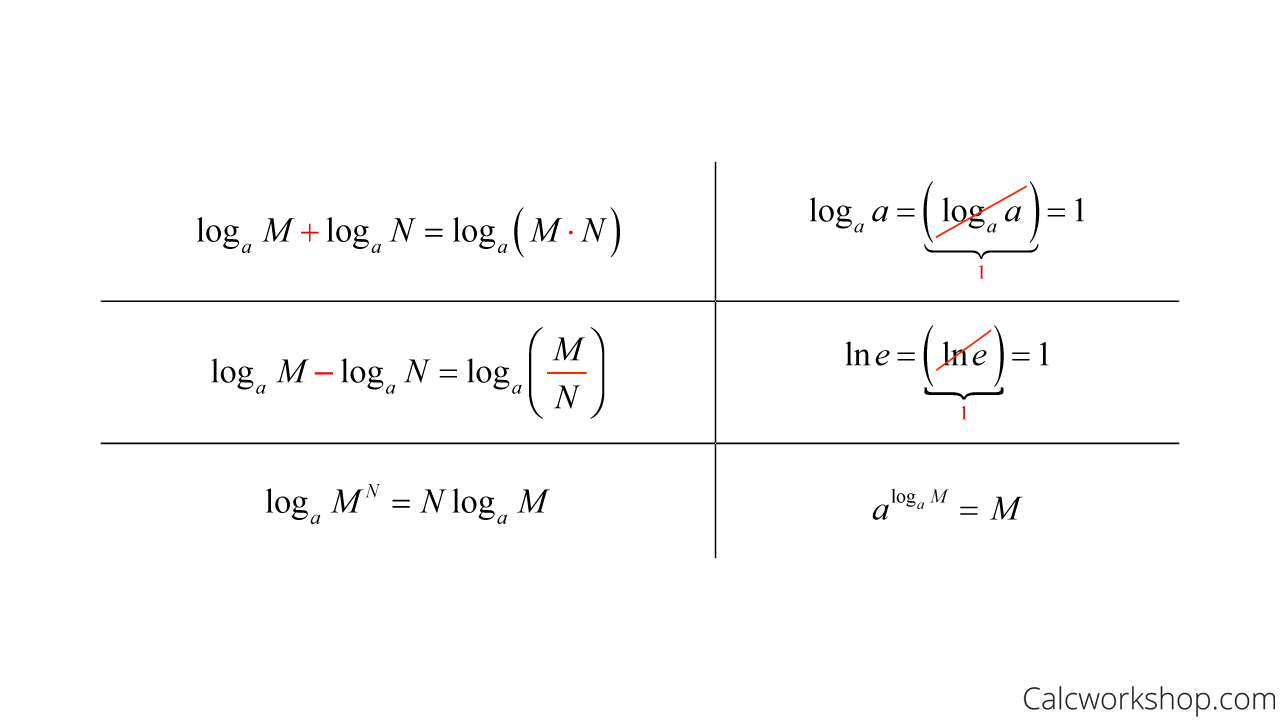
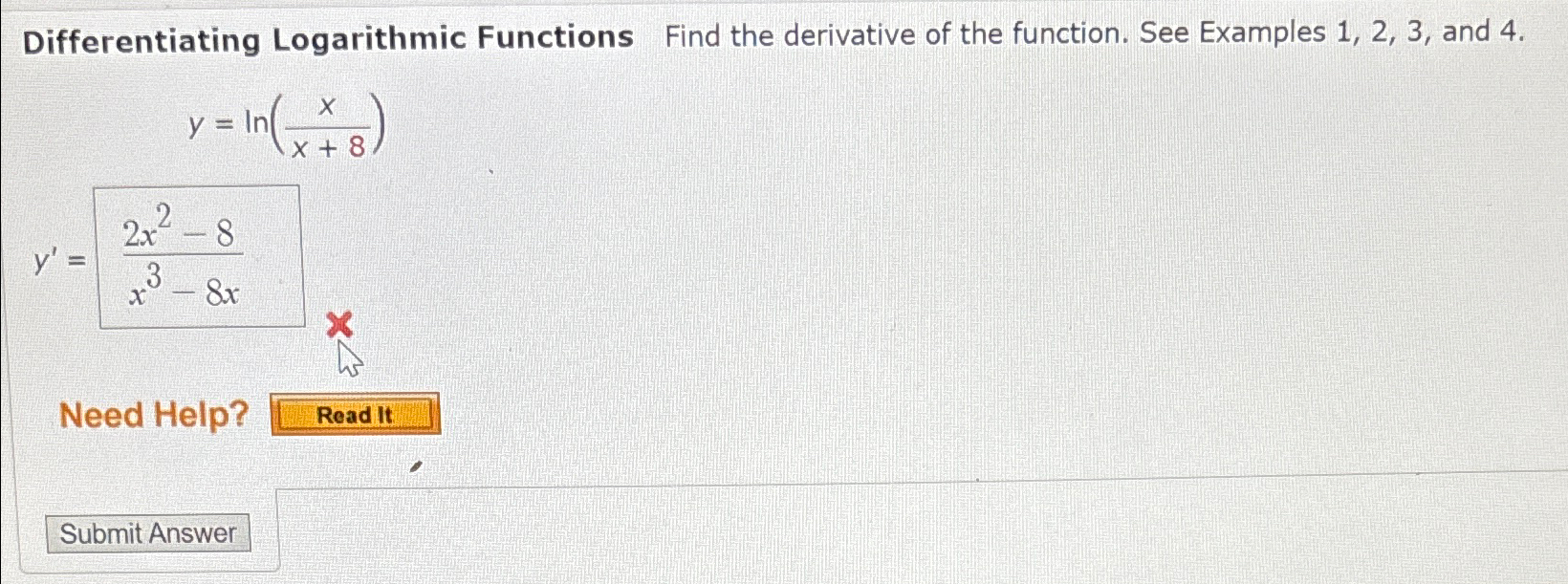
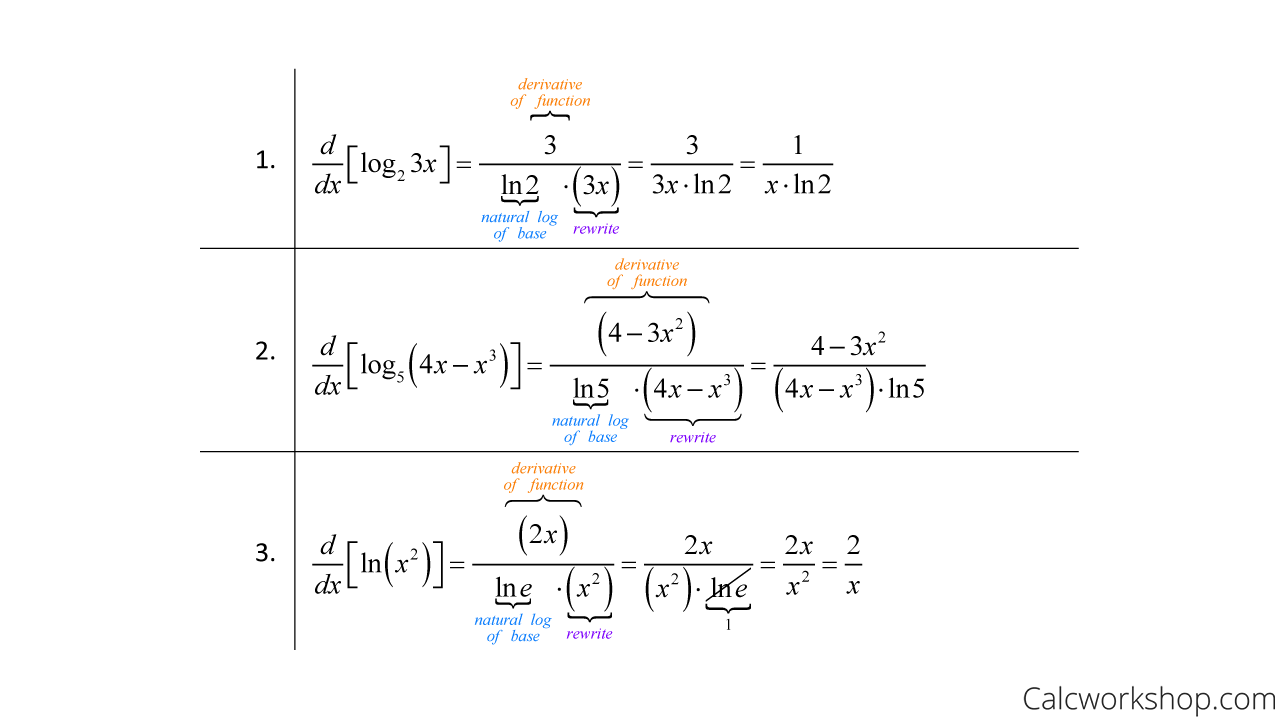
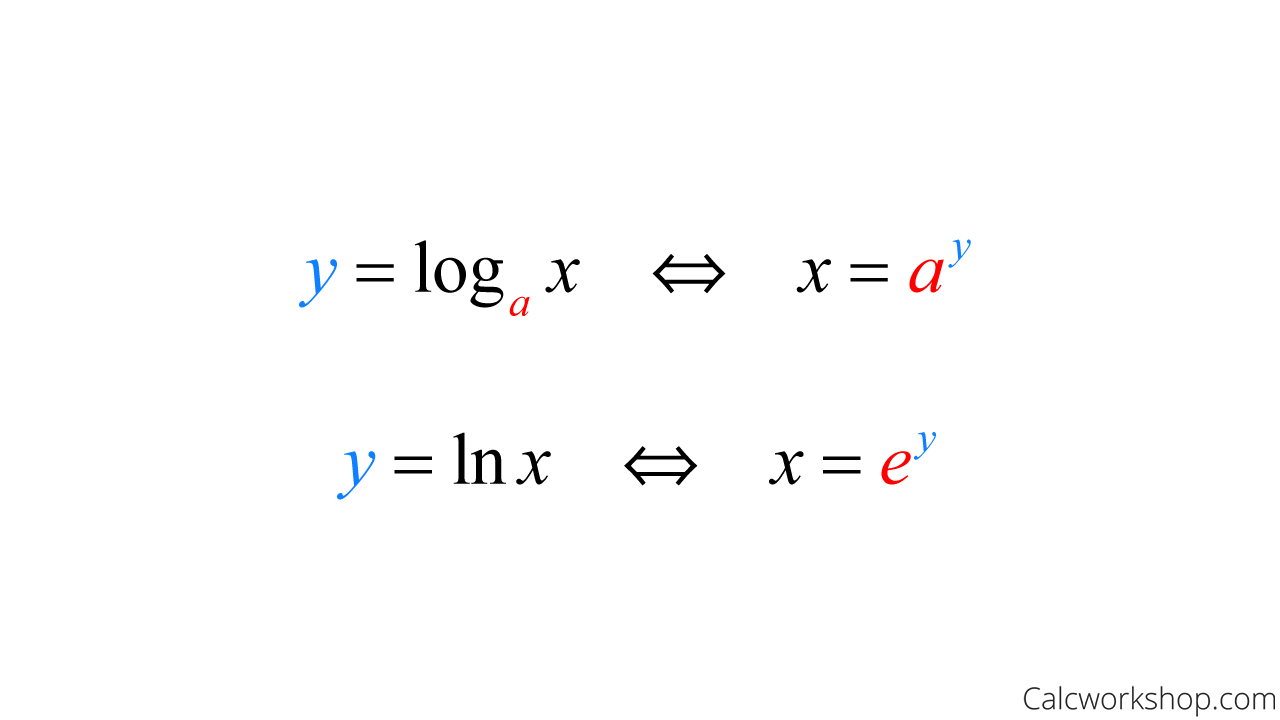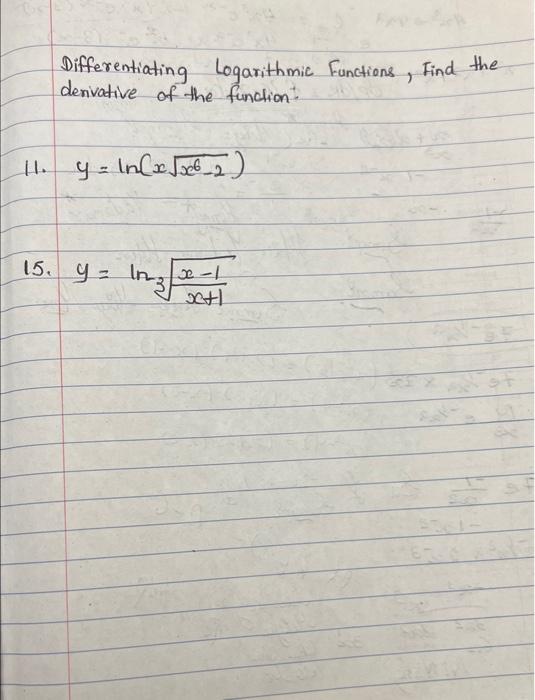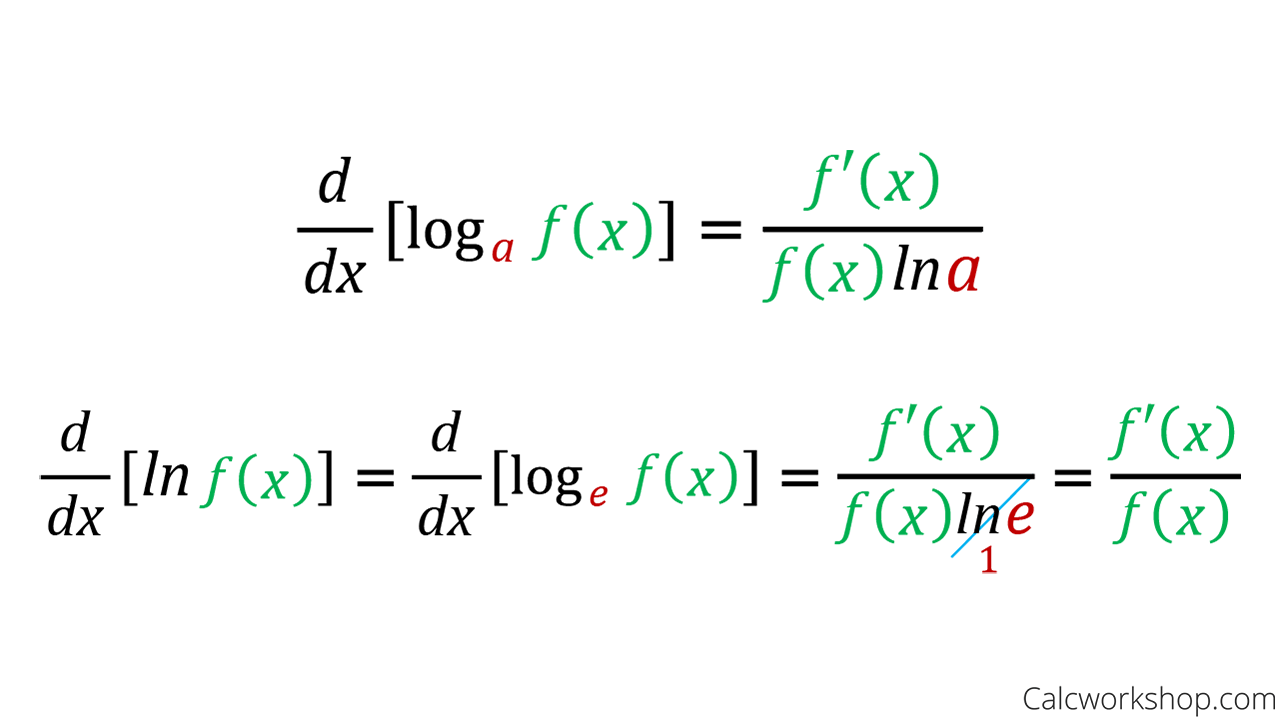Differentiating Logarithmic Functions - Derivatives of logarithmic functions are mainly based on the chain rule. However, we can generalize it for any differentiable function with. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. Logarithmic differentiation gives an alternative method for. In this section we will discuss logarithmic differentiation.
In this section we will discuss logarithmic differentiation. Logarithmic differentiation gives an alternative method for. However, we can generalize it for any differentiable function with. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. Derivatives of logarithmic functions are mainly based on the chain rule. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by.
In this section we will discuss logarithmic differentiation. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. Derivatives of logarithmic functions are mainly based on the chain rule. Logarithmic differentiation gives an alternative method for. However, we can generalize it for any differentiable function with. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by.
Derivatives of Logarithmic Functions (Fully Explained!)
Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. In this section we will discuss logarithmic differentiation. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. Logarithmic differentiation gives an alternative method for. However, we can generalize it for any differentiable function with.
Question Video Logarithmic Differentiation Of Functions, 40 OFF
In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. In this section we will discuss logarithmic differentiation. However, we can generalize it for any differentiable function with. Logarithmic differentiation gives an alternative method for. Derivatives of logarithmic functions are mainly based on the chain rule.
Derivatives of Logarithmic Functions (Fully Explained!)
However, we can generalize it for any differentiable function with. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. Logarithmic differentiation gives an alternative method for. In this section we will discuss logarithmic differentiation. Derivatives of logarithmic functions are mainly based on the chain rule.
Solved Differentiating Logarithmic FunctionsFind the
However, we can generalize it for any differentiable function with. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. Logarithmic differentiation gives an alternative method for. In this section we will discuss logarithmic differentiation. Derivatives of logarithmic functions are mainly based on the chain rule.
Solved Differentiating logarithmic functions Use
Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. In this section we will discuss logarithmic differentiation. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. Logarithmic differentiation gives an alternative method for. However, we can generalize it for any differentiable function with.
Differentiating Logarithmic and Exponential Functions PDF
In this section we will discuss logarithmic differentiation. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. However, we can generalize it for any differentiable function with. Derivatives of logarithmic functions are mainly based.
Solved Differentiating Logarithmic Functions, Find the
Logarithmic differentiation gives an alternative method for. In this section we will discuss logarithmic differentiation. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. However, we can generalize it for any differentiable function with. Derivatives of logarithmic functions are mainly based on the chain rule.
Derivatives of Logarithmic Functions (Fully Explained!)
In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. In this section we will discuss logarithmic differentiation. Derivatives of logarithmic functions are mainly based on the chain rule. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Logarithmic differentiation gives an alternative method.
Derivatives of Logarithmic Functions (Fully Explained!)
However, we can generalize it for any differentiable function with. In this section we will discuss logarithmic differentiation. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Derivatives of logarithmic functions are mainly based.
Derivatives of Logarithmic Functions
Derivatives of logarithmic functions are mainly based on the chain rule. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the. However, we can generalize it for any differentiable function with. In this section we will discuss logarithmic differentiation. Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or.
In This Section We Will Discuss Logarithmic Differentiation.
Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by. Logarithmic differentiation gives an alternative method for. However, we can generalize it for any differentiable function with. In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the.