Differentiating Integrals - T) dx is a function of t, so we can ask about its t. We integrate over x and are left with something that depends only on t, not x. Under fairly loose conditions on the. We derive one of euler’s formulas by employing the trick of differentiating under the integral sign. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. I learned about this method from the website of.
We derive one of euler’s formulas by employing the trick of differentiating under the integral sign. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Under fairly loose conditions on the. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. T) dx is a function of t, so we can ask about its t. I learned about this method from the website of. We integrate over x and are left with something that depends only on t, not x.
We integrate over x and are left with something that depends only on t, not x. Under fairly loose conditions on the. We derive one of euler’s formulas by employing the trick of differentiating under the integral sign. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. I learned about this method from the website of. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. T) dx is a function of t, so we can ask about its t.
Integrals ONE GREAT WORLD FOR ALL
Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Under fairly loose conditions on the. We integrate over x and are left with something that depends.
List of Integrals Containing ln
T) dx is a function of t, so we can ask about its t. Under fairly loose conditions on the. I learned about this method from the website of. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. We integrate over x and are left with something that depends only on t, not x.
Solved Differentiating Integrals Under mild continuity
Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. T) dx is a function of t, so we can ask about its t. We derive one of euler’s formulas by employing the trick of differentiating under the integral sign. Unless the variable x appears in either (or both) of the limits of integration, the.
[1st year uni calculus] Differentiating integrals with chain rule r
Under fairly loose conditions on the. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. We integrate over x and are left with something that depends only on t, not x. We derive one of euler’s formulas by employing the trick.
Solved Exercise 2.11 Differentiating integrals Use the
Under fairly loose conditions on the. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. We integrate over x and are left with something that depends only on t, not x. I learned about this method from the website of. Unless the variable x appears in either (or both) of the limits of integration,.
Indefinite Integrals 7 VividMath — US..
Under fairly loose conditions on the. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. I learned about this method from the website of. We integrate over x and are left with something that depends only on t, not x. We derive one of euler’s formulas by employing the trick of differentiating under the.
DIFFERENTIATING INTEGRALS OR INTEGRATING DERIVATIVES Transport Phenomena
Under fairly loose conditions on the. T) dx is a function of t, so we can ask about its t. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. We integrate over x and are left with something that depends only.
Calculus Integrals Reference Sheet (with Formulas) EEWeb
We integrate over x and are left with something that depends only on t, not x. T) dx is a function of t, so we can ask about its t. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. Unless the variable x appears in either (or both) of the limits of integration, the.
Definite Integrals 3 VividMath — US..
We integrate over x and are left with something that depends only on t, not x. Under fairly loose conditions on the. Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative. I learned about this method from the website of. T).
Definite Integrals 5 VividMath — US..
Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. I learned about this method from the website of. T) dx is a function of t, so we can ask about its t. We integrate over x and are left with something that depends only on t, not x. Under fairly loose conditions on the.
Under Fairly Loose Conditions On The.
I learned about this method from the website of. Differentiation under the integral sign is an operation in calculus used to evaluate certain integrals. We derive one of euler’s formulas by employing the trick of differentiating under the integral sign. T) dx is a function of t, so we can ask about its t.
We Integrate Over X And Are Left With Something That Depends Only On T, Not X.
Unless the variable x appears in either (or both) of the limits of integration, the result of the definite integral will not involve x, and so the derivative.
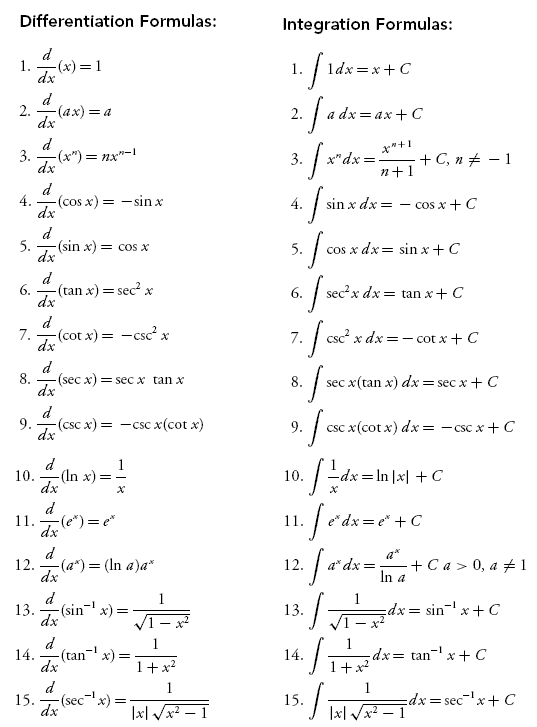
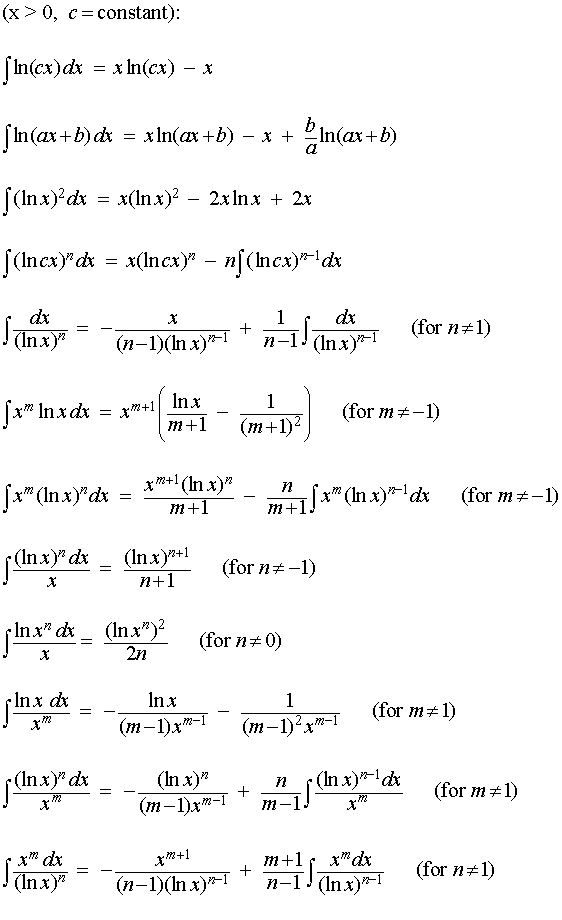

![[1st year uni calculus] Differentiating integrals with chain rule r](https://i.imgur.com/P5cyd16.png)





