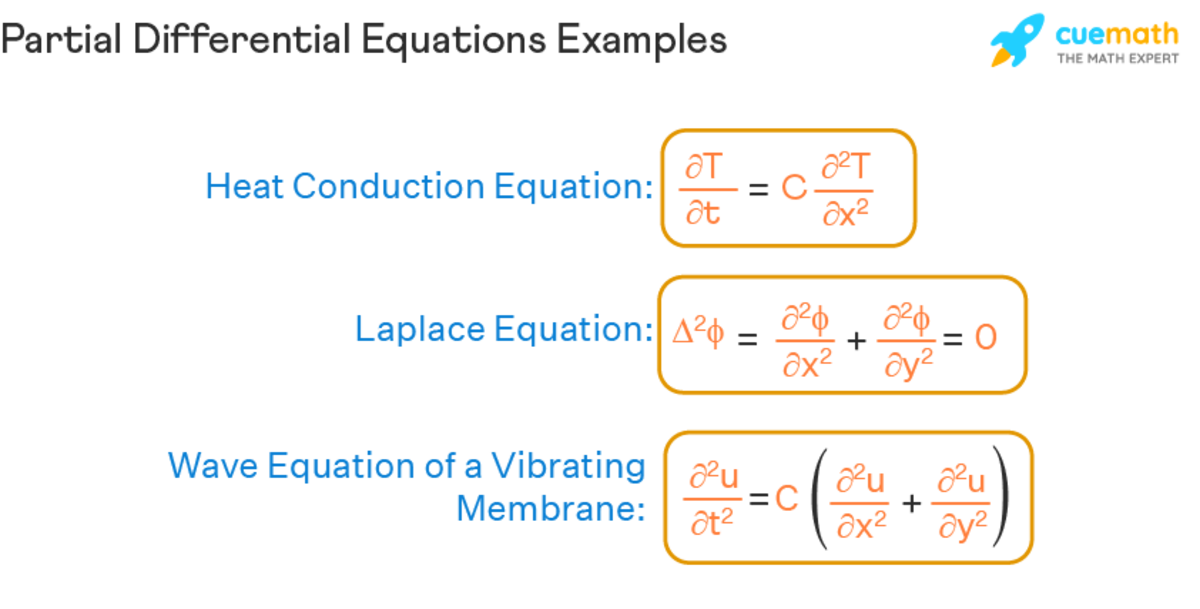
Differential Equations Temperature

Differential Equations Temperature - Three physical principles are used here. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Heat (or thermal) energy of a body with uniform properties:. Introduction to solving partial differential equations. In this section, we explore the method. In this section we will do a partial derivation of the heat equation that can be solved.

Introduction to solving partial differential equations. In this section, we explore the method. Heat (or thermal) energy of a body with uniform properties:. Three physical principles are used here. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. In this section we will do a partial derivation of the heat equation that can be solved.

Introduction to solving partial differential equations. Three physical principles are used here. In this section, we explore the method. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. In this section we will do a partial derivation of the heat equation that can be solved. Heat (or thermal) energy of a body with uniform properties:.

Differential Equations Owlcation

The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Three physical principles are used here. In this section, we explore the method. In this section we will do a partial derivation of the heat equation that can be solved. Heat (or thermal) energy of a body with uniform properties:.

Differential Equations Owlcation

Three physical principles are used here. In this section, we explore the method. In this section we will do a partial derivation of the heat equation that can be solved. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Heat (or thermal) energy of a body with uniform properties:.

differential equations

Heat (or thermal) energy of a body with uniform properties:. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Introduction to solving partial differential equations. In this section we will do a partial derivation of the heat equation that can be solved. Three physical principles are used here.

Textbooks Differential Equations Freeup

In this section we will do a partial derivation of the heat equation that can be solved. Three physical principles are used here. Introduction to solving partial differential equations. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. In this section, we explore the method.

Worksheet 8 Problems Differential Equation MATH 165 Study

Heat (or thermal) energy of a body with uniform properties:. Three physical principles are used here. Introduction to solving partial differential equations. In this section we will do a partial derivation of the heat equation that can be solved. In this section, we explore the method.

22Differential Equation01 Theory PDF Equations Temperature

In this section, we explore the method. In this section we will do a partial derivation of the heat equation that can be solved. Heat (or thermal) energy of a body with uniform properties:. Three physical principles are used here. Introduction to solving partial differential equations.

Differential Equations Flashcards Memorang

Heat (or thermal) energy of a body with uniform properties:. In this section we will do a partial derivation of the heat equation that can be solved. In this section, we explore the method. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Introduction to solving partial differential equations.

Differential Equations

In this section we will do a partial derivation of the heat equation that can be solved. Introduction to solving partial differential equations. In this section, we explore the method. Three physical principles are used here. Heat (or thermal) energy of a body with uniform properties:.

calculus Differential equations temperature change and room

Introduction to solving partial differential equations. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Heat (or thermal) energy of a body with uniform properties:. Three physical principles are used here. In this section, we explore the method.

Modelling with Differential Equations Temperature Change

Three physical principles are used here. Heat (or thermal) energy of a body with uniform properties:. Introduction to solving partial differential equations. In this section, we explore the method. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u.

The Temperature Is Modeled By The Heat Equation (Seesubsection 7.1For A Derivation) @U @T = @2U.

Three physical principles are used here. Heat (or thermal) energy of a body with uniform properties:. In this section we will do a partial derivation of the heat equation that can be solved. Introduction to solving partial differential equations.