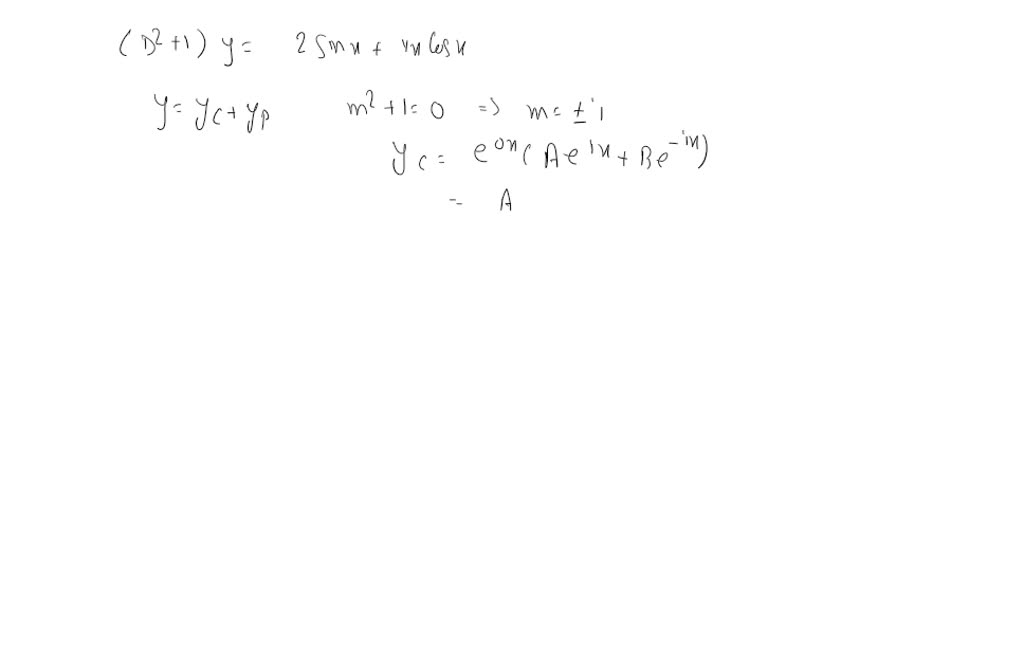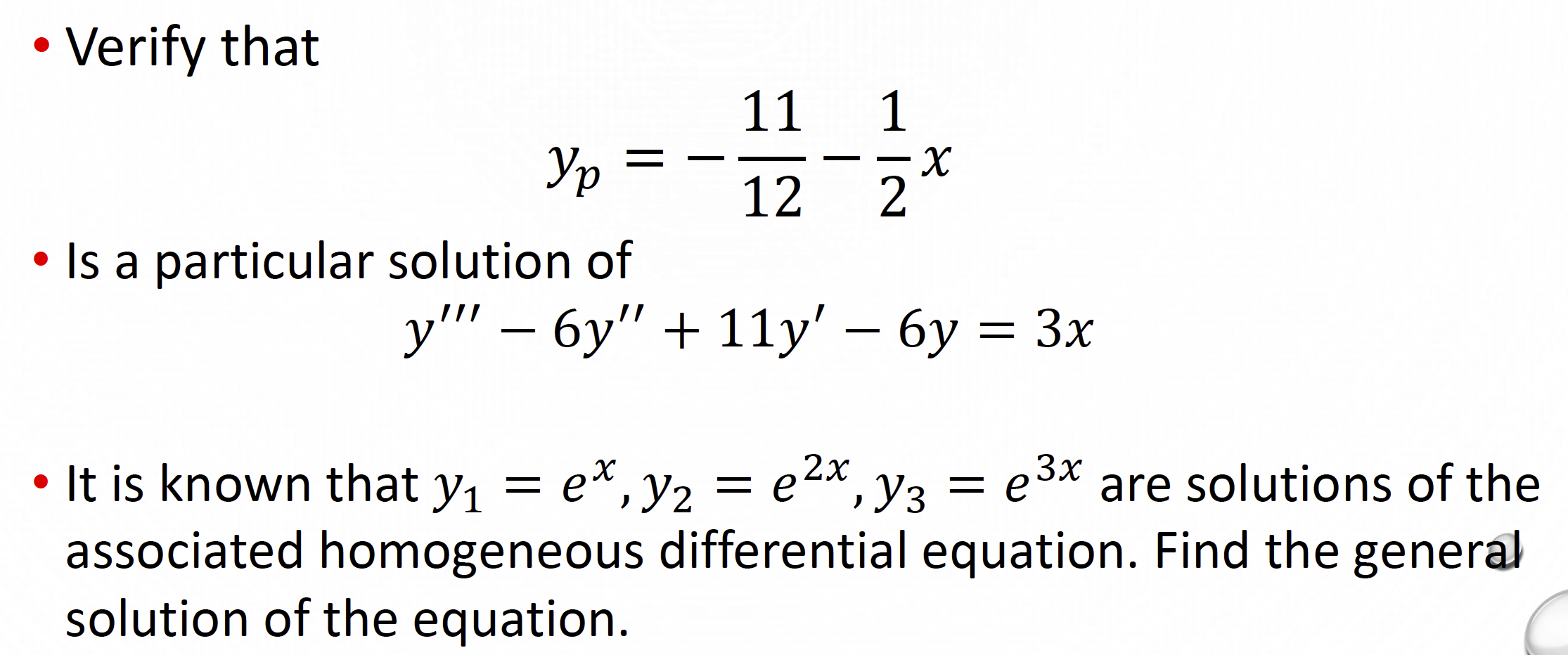Differential Equations Superposition - In this section give an in depth discussion on the process used to solve. Suppose that we have a linear homogenous second order. Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the. Superposition principle ocw 18.03sc ii. + 2x = e−2t has a solution x(t) = te−2t iii. + 2x = 0 has. If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any. The principle of superposition states that \(x = x(t)\) is also a solution of.
In this section give an in depth discussion on the process used to solve. Suppose that we have a linear homogenous second order. + 2x = e−2t has a solution x(t) = te−2t iii. The principle of superposition states that \(x = x(t)\) is also a solution of. Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the. + 2x = 0 has. Superposition principle ocw 18.03sc ii. If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any.
If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any. Suppose that we have a linear homogenous second order. Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the. In this section give an in depth discussion on the process used to solve. + 2x = 0 has. Superposition principle ocw 18.03sc ii. The principle of superposition states that \(x = x(t)\) is also a solution of. + 2x = e−2t has a solution x(t) = te−2t iii.
SOLVEDSolve the given differential equations by using the principle of
Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the. + 2x = 0 has. + 2x = e−2t has a solution x(t) = te−2t iii. Superposition principle ocw 18.03sc ii. The principle of superposition states that \(x = x(t)\) is also a solution of.
Solved Differential Equations Superposition principle
Suppose that we have a linear homogenous second order. Superposition principle ocw 18.03sc ii. If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any. + 2x = 0 has. Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the.
Proof superposition principle differential equations alaskakery
In this section give an in depth discussion on the process used to solve. If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any. + 2x = 0 has. Suppose that we have a linear homogenous second order. Superposition principle ocw 18.03sc ii.
Section 2.4Superposition PDF Partial Differential Equation
Suppose that we have a linear homogenous second order. + 2x = e−2t has a solution x(t) = te−2t iii. Superposition principle ocw 18.03sc ii. The principle of superposition states that \(x = x(t)\) is also a solution of. If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any.
Principle of Superposition and Linear Independence Download Free PDF
+ 2x = 0 has. Superposition principle ocw 18.03sc ii. Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the. Suppose that we have a linear homogenous second order. In this section give an in depth discussion on the process used to solve.
Solved Solve these differential equations by 1 Superposition
The principle of superposition states that \(x = x(t)\) is also a solution of. + 2x = 0 has. If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any. In this section give an in depth discussion on the process used to solve. Thus, by superposition principle, the general solution to a nonhomogeneous equation.
SuperpositionDifferential EquationsAssignemnt and Solution Docsity
Suppose that we have a linear homogenous second order. + 2x = e−2t has a solution x(t) = te−2t iii. Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the. In this section give an in depth discussion on the process used to solve. If y1 and y2 are solutions of a homogeneous linear.
(PDF) Superposition rules, lie theorem, and partial differential
Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the. Suppose that we have a linear homogenous second order. Superposition principle ocw 18.03sc ii. If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any. In this section give an in depth discussion on the process used to solve.
(PDF) Superposition rules and secondorder differential equations
If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any. + 2x = e−2t has a solution x(t) = te−2t iii. Superposition principle ocw 18.03sc ii. The principle of superposition states that \(x = x(t)\) is also a solution of. Suppose that we have a linear homogenous second order.
(PDF) Superposition principle and schemes for Measure Differential
+ 2x = 0 has. If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any. Superposition principle ocw 18.03sc ii. + 2x = e−2t has a solution x(t) = te−2t iii. Suppose that we have a linear homogenous second order.
The Principle Of Superposition States That \(X = X(T)\) Is Also A Solution Of.
If y1 and y2 are solutions of a homogeneous linear equa tion, then so is any. In this section give an in depth discussion on the process used to solve. Suppose that we have a linear homogenous second order. Thus, by superposition principle, the general solution to a nonhomogeneous equation is the sum of the.
+ 2X = E−2T Has A Solution X(T) = Te−2T Iii.
+ 2x = 0 has. Superposition principle ocw 18.03sc ii.