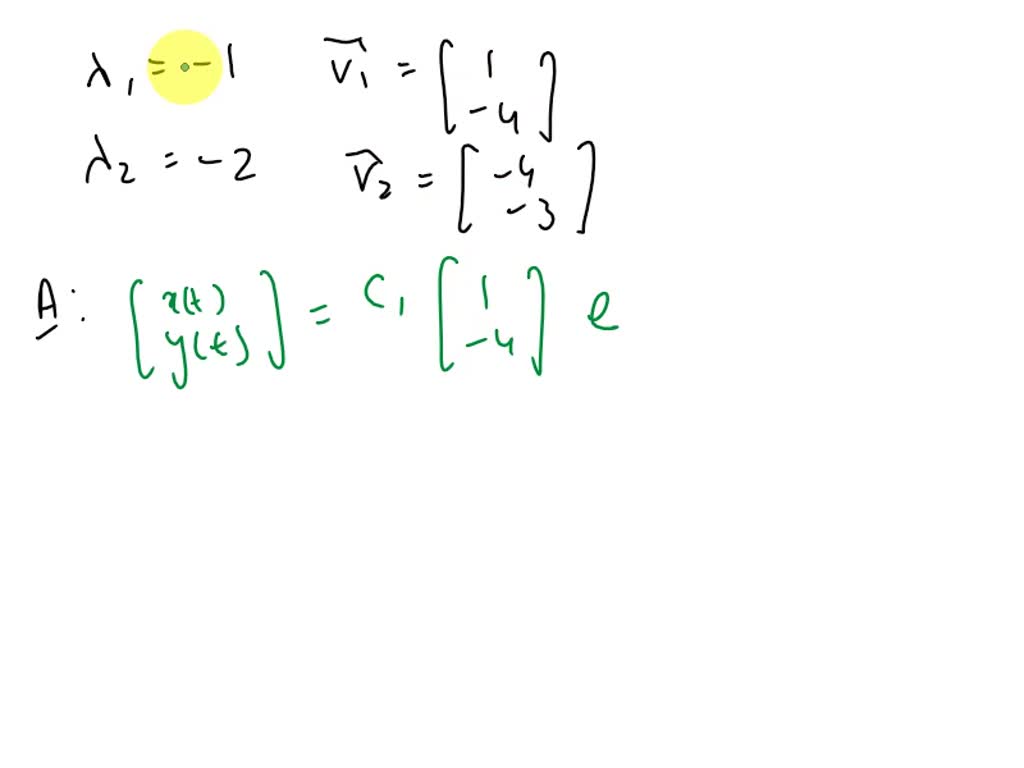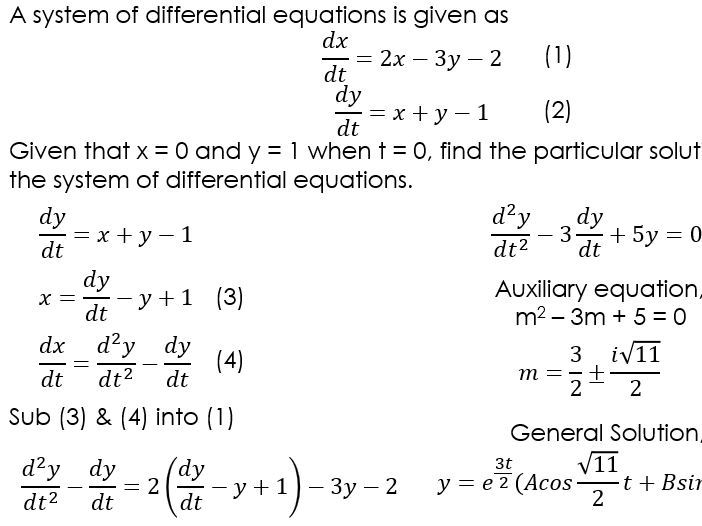Differential Equations Eigenvectors - (a − λi)→v = →0, and. This chapter ends by solving linear differential equations du/dt = au. In this section we will introduce the concept of eigenvalues and eigenvectors of a. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. So lets’ solve ax = 2x: We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : The pieces of the solution. To find an eigenvector corresponding to an eigenvalue λ, we write. But we need a method to compute eigenvectors.
This chapter ends by solving linear differential equations du/dt = au. This is back to last week,. The pieces of the solution. In this section we will introduce the concept of eigenvalues and eigenvectors of a. (a − λi)→v = →0, and. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : To find an eigenvector corresponding to an eigenvalue λ, we write. But we need a method to compute eigenvectors. So lets’ solve ax = 2x:
(a − λi)→v = →0, and. But we need a method to compute eigenvectors. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. So lets’ solve ax = 2x: The pieces of the solution. This chapter ends by solving linear differential equations du/dt = au. This is back to last week,. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. To find an eigenvector corresponding to an eigenvalue λ, we write. In this section we will introduce the concept of eigenvalues and eigenvectors of a.
Differential Equation and Linear Algebra (MA11001) PDF Eigenvalues
So lets’ solve ax = 2x: The pieces of the solution. This chapter ends by solving linear differential equations du/dt = au. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. In this section we will introduce the concept of eigenvalues and eigenvectors of a.
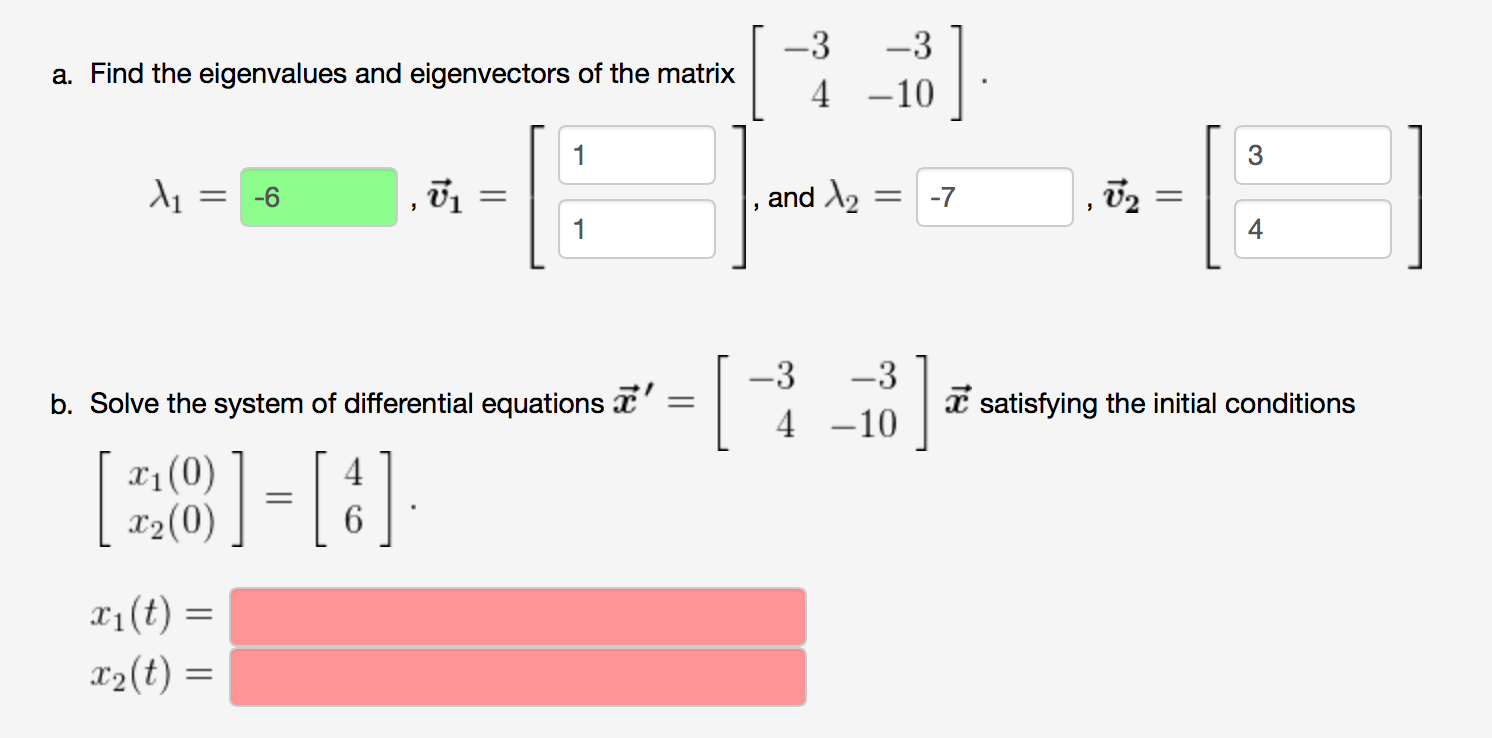
Solved a. Find the eigenvalues and eigenvectors of the
So lets’ solve ax = 2x: (a − λi)→v = →0, and. This is back to last week,. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. In this section we will introduce the concept of eigenvalues and eigenvectors of a.
(PDF) Differential Equations Review _ Eigenvalues & Eigenvectors
This is back to last week,. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : (a − λi)→v = →0, and. But we need a method to compute eigenvectors. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
linear algebra Using eigenvectors and values to get systems of
This chapter ends by solving linear differential equations du/dt = au. In this section we will introduce the concept of eigenvalues and eigenvectors of a. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : Understanding eigenvalues and eigenvectors is essential for solving systems of differential. So lets’ solve ax.
Solved Application of eigenvalues and eigenvectors to
The pieces of the solution. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : So lets’ solve ax = 2x: This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
SOLVED Differential Equations Suppose that the matrix A has the
(a − λi)→v = →0, and. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. This is back to last week,. To find an eigenvector corresponding to an eigenvalue λ, we write. This chapter ends by solving linear differential equations du/dt = au.
On Derivatives of Eigenvalues and Eigenvectors of The Download Free
This is back to last week,. In this section we will introduce the concept of eigenvalues and eigenvectors of a. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : So lets’ solve ax = 2x: This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
Solved Solve the given system of differential equations
Understanding eigenvalues and eigenvectors is essential for solving systems of differential. But we need a method to compute eigenvectors. This is back to last week,. In this section we will introduce the concept of eigenvalues and eigenvectors of a. So lets’ solve ax = 2x:
Differential Equations Problems and Solutions Stability Theory
This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role. (a − λi)→v = →0, and. Understanding eigenvalues and eigenvectors is essential for solving systems of differential. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) : This chapter ends by solving linear differential equations du/dt =.
Modelling with differential equations Teaching Resources
The pieces of the solution. So lets’ solve ax = 2x: This chapter ends by solving linear differential equations du/dt = au. To find an eigenvector corresponding to an eigenvalue λ, we write. We want y1 and y2 to grow or decay in exactly the same way (with the same e t) :
In This Section We Will Introduce The Concept Of Eigenvalues And Eigenvectors Of A.
But we need a method to compute eigenvectors. (a − λi)→v = →0, and. To find an eigenvector corresponding to an eigenvalue λ, we write. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role.
We Want Y1 And Y2 To Grow Or Decay In Exactly The Same Way (With The Same E T) :
Understanding eigenvalues and eigenvectors is essential for solving systems of differential. So lets’ solve ax = 2x: This chapter ends by solving linear differential equations du/dt = au. This is back to last week,.