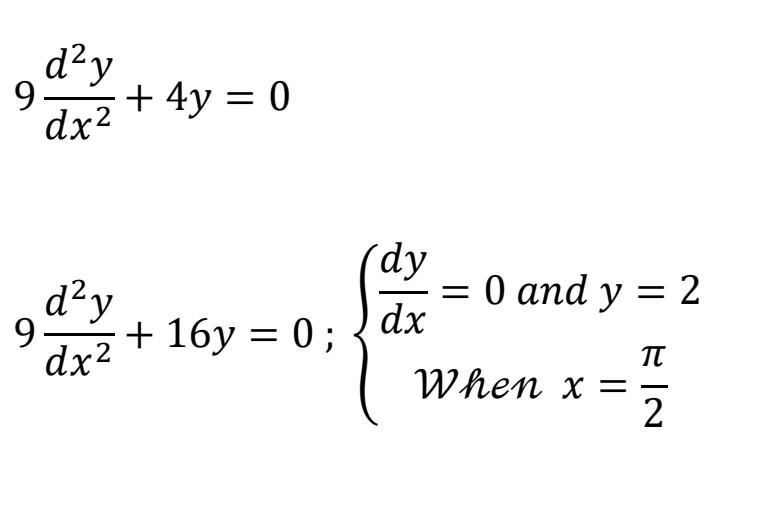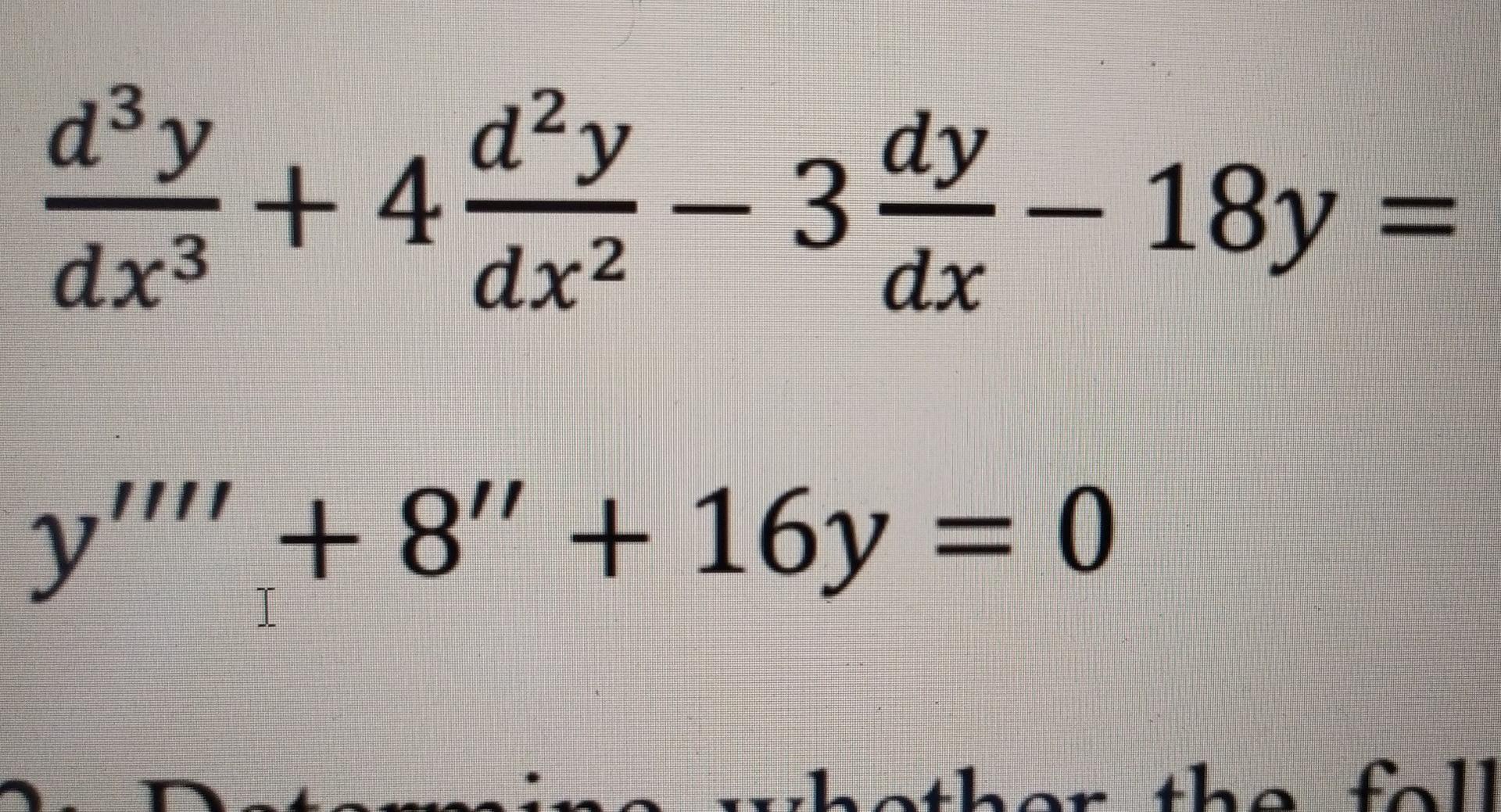Differential Equations Auxiliary Equation - K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. The auxiliary equation is easily found to be: Equation (12.9) is called the auxiliary equation of the differential equation (12.10). In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of.
The auxiliary equation is easily found to be: Equation (12.9) is called the auxiliary equation of the differential equation (12.10). K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of.
The auxiliary equation is easily found to be: In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. Equation (12.9) is called the auxiliary equation of the differential equation (12.10).
[Solved] The auxiliary equation for the given differential equation has
K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. Equation (12.9) is called the auxiliary equation of the differential equation (12.10). The auxiliary equation is easily found to be:
SOLUTION Differential equations auxiliary equation example higher
Equation (12.9) is called the auxiliary equation of the differential equation (12.10). The auxiliary equation is easily found to be: K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of.
Differential Equations Solved Examples The roots of an auxiliary
Equation (12.9) is called the auxiliary equation of the differential equation (12.10). In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. The auxiliary equation is easily found to be:
Solved solve the differential equations, auxiliary equation
In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. Equation (12.9) is called the auxiliary equation of the differential equation (12.10). The auxiliary equation is easily found to be: K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have.
[Solved] The auxiliary equation for the given differential equation has
In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. The auxiliary equation is easily found to be: Equation (12.9) is called the auxiliary equation of the differential equation (12.10).
[Solved] The auxiliary equation for the given differential equation has
K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. The auxiliary equation is easily found to be: In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. Equation (12.9) is called the auxiliary equation of the differential equation (12.10).
[Solved] . 3. The auxiliary equation of the differential equation (D2 u
The auxiliary equation is easily found to be: K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. Equation (12.9) is called the auxiliary equation of the differential equation (12.10).
Solved what is the corresponding auxiliary equation of the
The auxiliary equation is easily found to be: In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. Equation (12.9) is called the auxiliary equation of the differential equation (12.10).
SOLUTION Differential equations auxiliary equation higher order linear
In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. Equation (12.9) is called the auxiliary equation of the differential equation (12.10). The auxiliary equation is easily found to be: K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have.
SOLUTION Auxiliary equation example higher order linear differential
K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. Equation (12.9) is called the auxiliary equation of the differential equation (12.10). The auxiliary equation is easily found to be:
Equation (12.9) Is Called The Auxiliary Equation Of The Differential Equation (12.10).
K2 + 4 = 0 that is, k2 = −4 so that k = ±2i, that is, we have. In mathematics, the characteristic equation (or auxiliary equation [1]) is an algebraic equation of. The auxiliary equation is easily found to be: