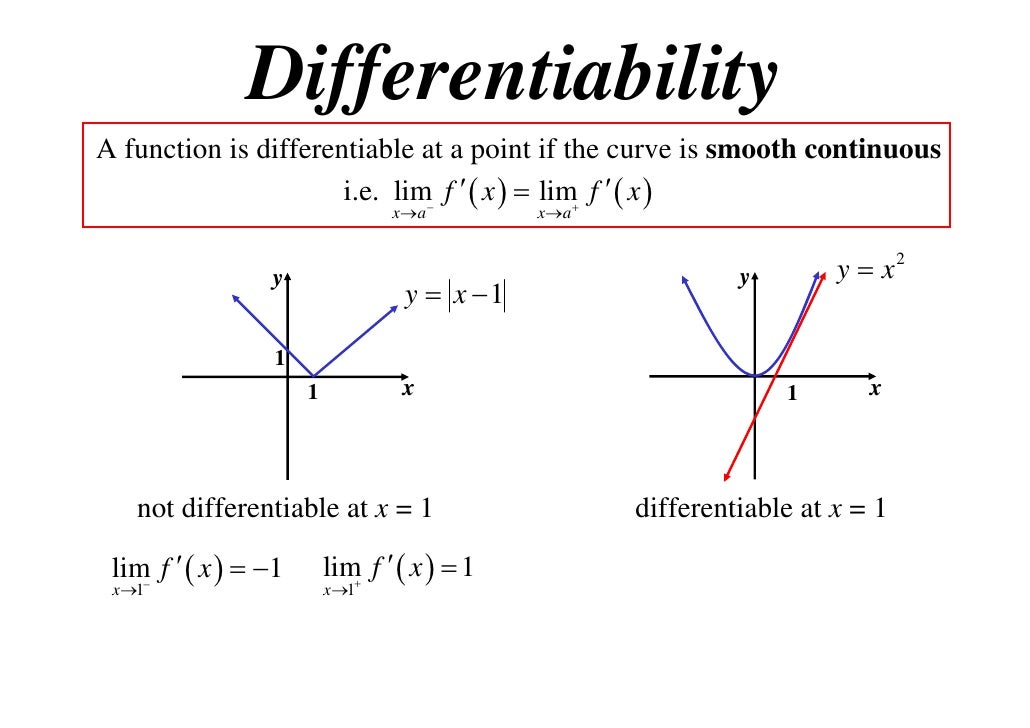
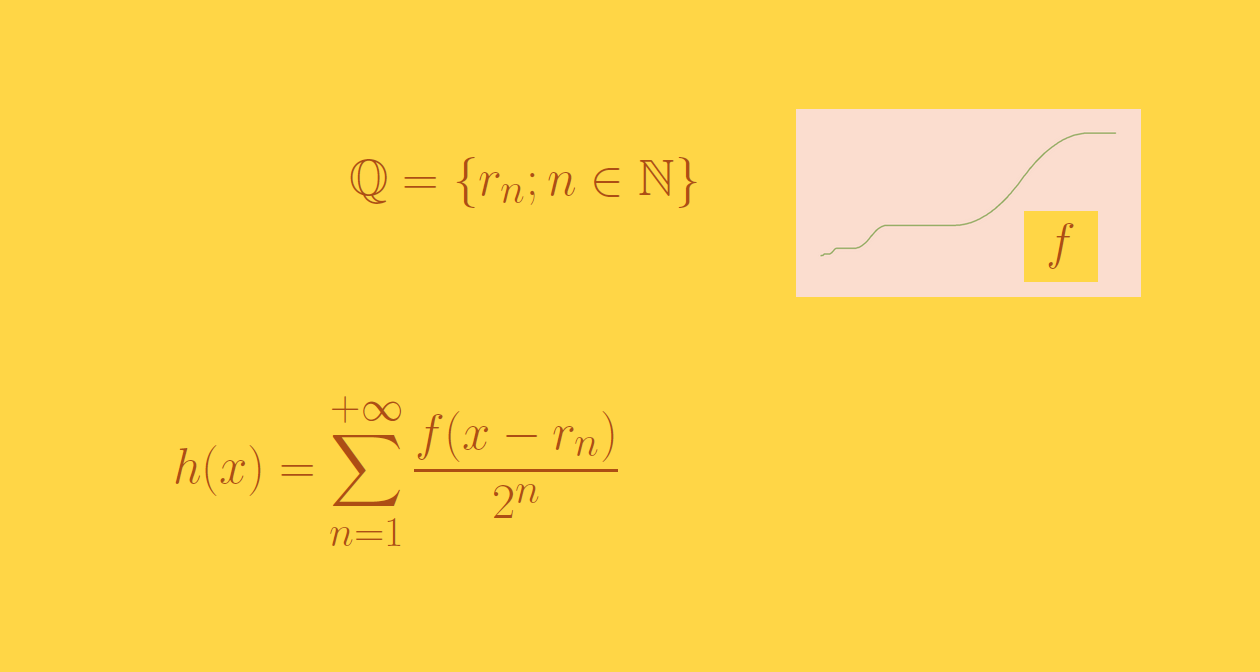Differentiable But Not Continuous - In one direction, the straight forward idea holds: If a function is differentiable at a point, then it must. I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable. Diverges, so that f ′ (x) is not continuous, even though it is defined for every.
I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable. Diverges, so that f ′ (x) is not continuous, even though it is defined for every. If a function is differentiable at a point, then it must. In one direction, the straight forward idea holds:
If a function is differentiable at a point, then it must. In one direction, the straight forward idea holds: Diverges, so that f ′ (x) is not continuous, even though it is defined for every. I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable.
Differentiable vs. Continuous Functions Understanding the Distinctions
I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable. In one direction, the straight forward idea holds: If a function is differentiable at a point, then it must. Diverges, so that f ′ (x) is not continuous, even though it is defined for every.
Can Something Be Differentiable but Not Continuous Quant RL
In one direction, the straight forward idea holds: Diverges, so that f ′ (x) is not continuous, even though it is defined for every. If a function is differentiable at a point, then it must. I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable.
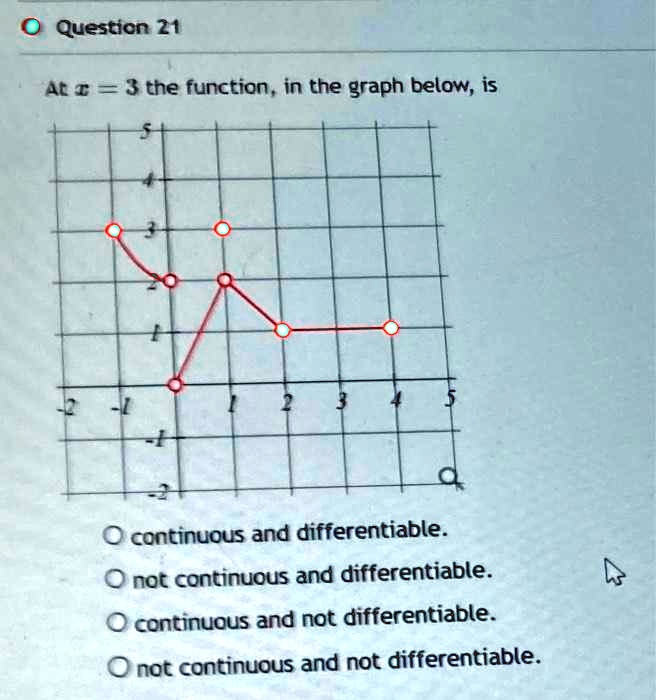
SOLVED The function in the graph below is Continuous and
If a function is differentiable at a point, then it must. Diverges, so that f ′ (x) is not continuous, even though it is defined for every. I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable. In one direction, the straight forward idea holds:
Can Something Be Differentiable but Not Continuous Quant RL
In one direction, the straight forward idea holds: Diverges, so that f ′ (x) is not continuous, even though it is defined for every. I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable. If a function is differentiable at a point, then it must.
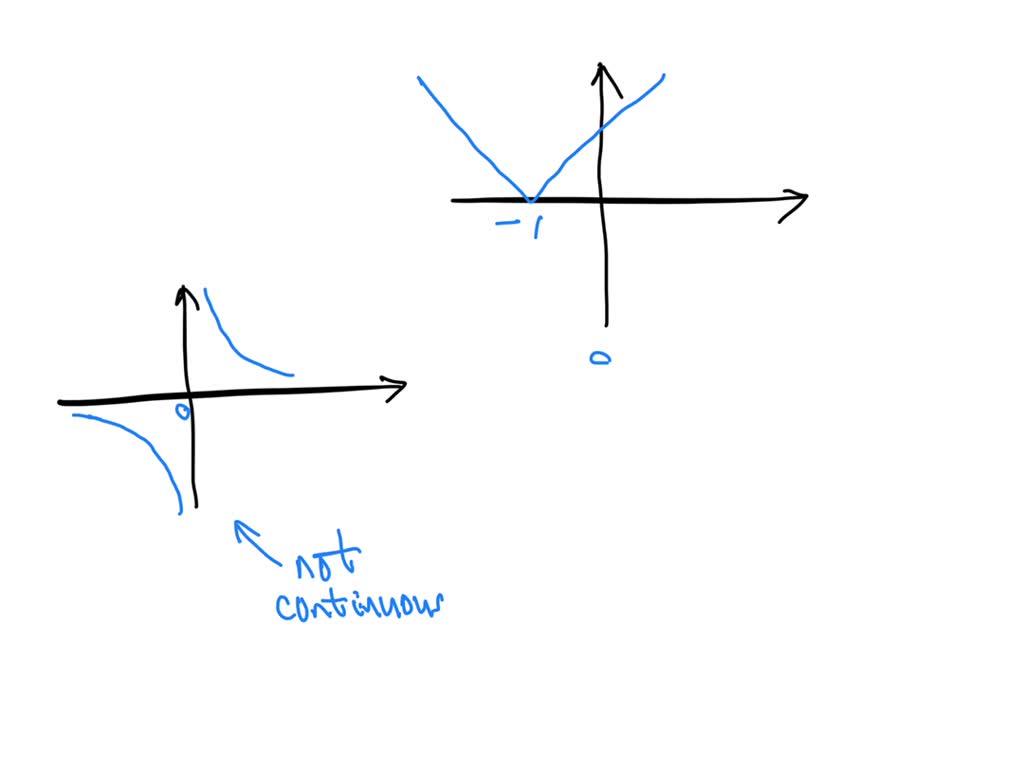
Continuous but Nowhere Differentiable Math Fun Facts
If a function is differentiable at a point, then it must. Diverges, so that f ′ (x) is not continuous, even though it is defined for every. In one direction, the straight forward idea holds: I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable.
(a) continuous everywhere but not differentiable (b) continuous and diffe..
In one direction, the straight forward idea holds: I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable. If a function is differentiable at a point, then it must. Diverges, so that f ′ (x) is not continuous, even though it is defined for every.
SOLVED The figure shows the graph of a function At the given value of
Diverges, so that f ′ (x) is not continuous, even though it is defined for every. I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable. If a function is differentiable at a point, then it must. In one direction, the straight forward idea holds:
The figure shows the graph of a function. At the given value of x, does
In one direction, the straight forward idea holds: Diverges, so that f ′ (x) is not continuous, even though it is defined for every. If a function is differentiable at a point, then it must. I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable.
When Is a Function Continuous but Not Differentiable Quant RL
In one direction, the straight forward idea holds: Diverges, so that f ′ (x) is not continuous, even though it is defined for every. If a function is differentiable at a point, then it must. I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable.
acontinuousfunctionnotdifferentiableontherationals
I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable. If a function is differentiable at a point, then it must. Diverges, so that f ′ (x) is not continuous, even though it is defined for every. In one direction, the straight forward idea holds:
In One Direction, The Straight Forward Idea Holds:
If a function is differentiable at a point, then it must. I am trying to prove f f is differentiable at x = 0 x = 0 but not continuously differentiable. Diverges, so that f ′ (x) is not continuous, even though it is defined for every.