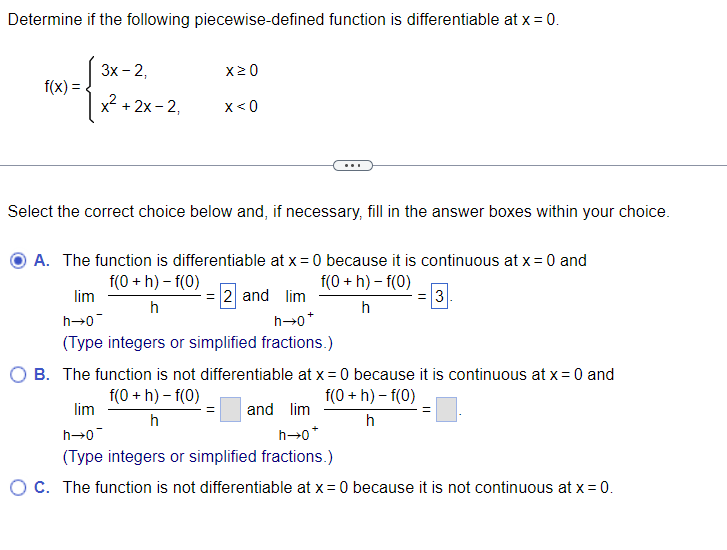
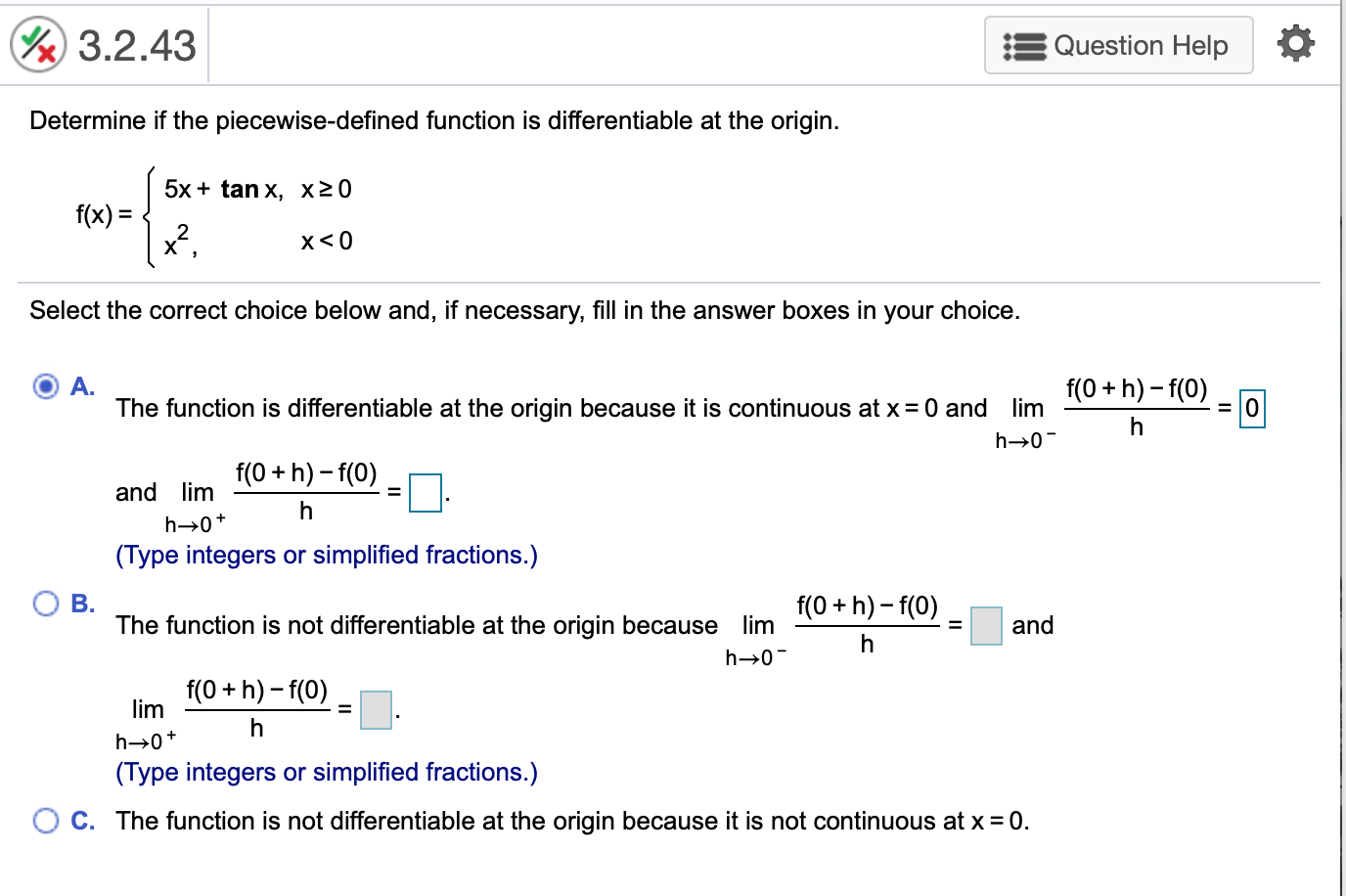
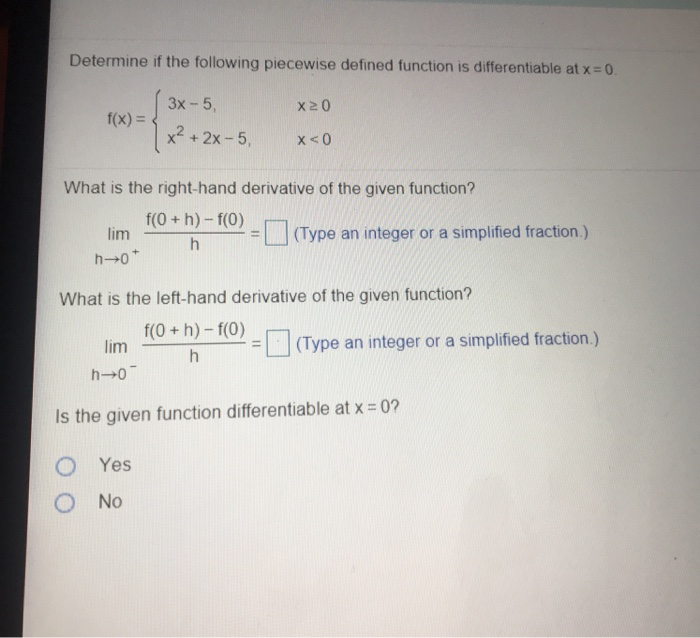
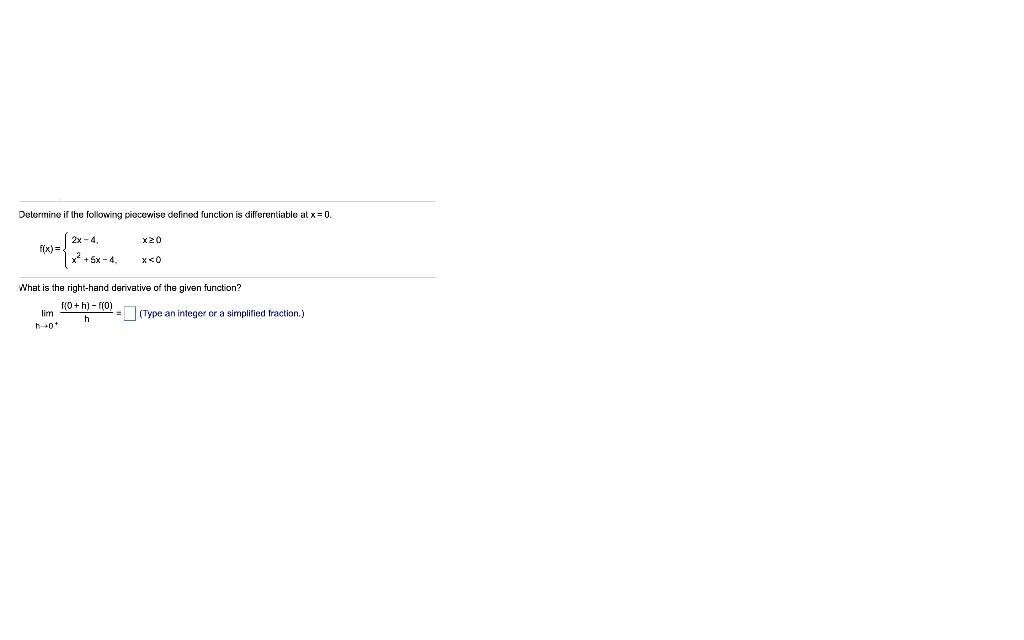
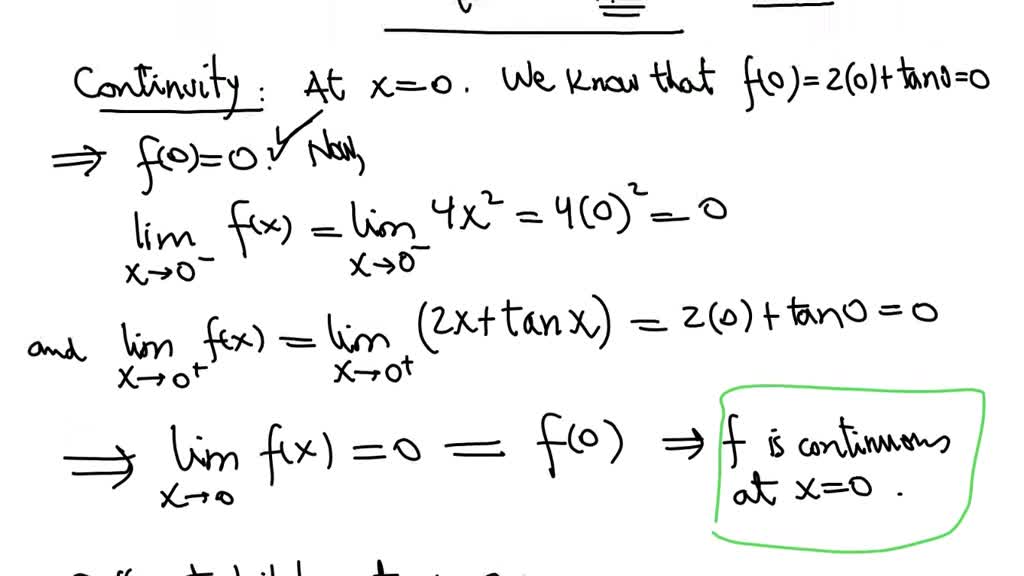Determine If The Piecewise-Defined Function Is Differentiable At The Origin - Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. (a) if f were differentiable at the origin, then: Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. Suppose p and q are defined on an open interval containing x=c, and each are. Is f differentiable at (0, 0)? Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y.
(a) if f were differentiable at the origin, then: Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. Suppose p and q are defined on an open interval containing x=c, and each are. Is f differentiable at (0, 0)? Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y.
Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. Suppose p and q are defined on an open interval containing x=c, and each are. Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. Is f differentiable at (0, 0)? (a) if f were differentiable at the origin, then:
Solved Determine if the following piecewisedefined function
Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. Suppose p and q are defined on an open interval containing x=c, and each are. Lim (s, t) → (0, 0) f (0 + s, 0 +.
SOLVED Determine if the piecewisedefined function is differentiable
(a) if f were differentiable at the origin, then: Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. Is f differentiable at (0, 0)? Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. Suppose p and q are defined on an open interval.
SOLVEDDetermine if the piecewisedefined function is differentiable at
Suppose p and q are defined on an open interval containing x=c, and each are. (a) if f were differentiable at the origin, then: Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. Lim (s, t).
Solved Determine if the piecewisedefined function is
Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. (a) if f were differentiable at the origin, then: Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. Suppose p and q are defined on an open interval containing x=c, and each are. Is.
Solved Determine if the piecewise defined function is
Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. Suppose p and q are defined on an open interval containing x=c, and each are. Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. Is f differentiable at (0, 0)? Generally, if you graph.
Solved 3.2.43 Question Help Determine if the
Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. Is f differentiable at (0, 0)? Suppose p and q are defined on an open interval containing x=c, and each are. Since for all.
Solved Determine if the following piecewise defined function
Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. (a) if f were differentiable at the origin, then: Is f differentiable at (0, 0)? Since for all x, y in r, f(x, 0).
Solved Determine if the piecewisedefined function is
Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. Suppose p and q are defined on an open interval containing x=c, and each are. Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. Lim (s, t) → (0, 0) f (0 + s, 0 +.
Determine if the piecewisedefined function is differentiable at the
Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. Suppose p and q are defined on an open interval containing x=c, and each are. Is f differentiable at (0, 0)? Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. (a) if f were differentiable at.
Solved Determine if the following piecewise defined function
Generally, if you graph a piecewise function and at any point it doesn't look smooth (there's a. Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. Suppose p and q are defined on an.
Generally, If You Graph A Piecewise Function And At Any Point It Doesn't Look Smooth (There's A.
Since for all x, y in r, f(x, 0) = 0 and f(0, y) = y. Lim (s, t) → (0, 0) f (0 + s, 0 + t) − f (0, 0) − 0,. (a) if f were differentiable at the origin, then: Suppose p and q are defined on an open interval containing x=c, and each are.