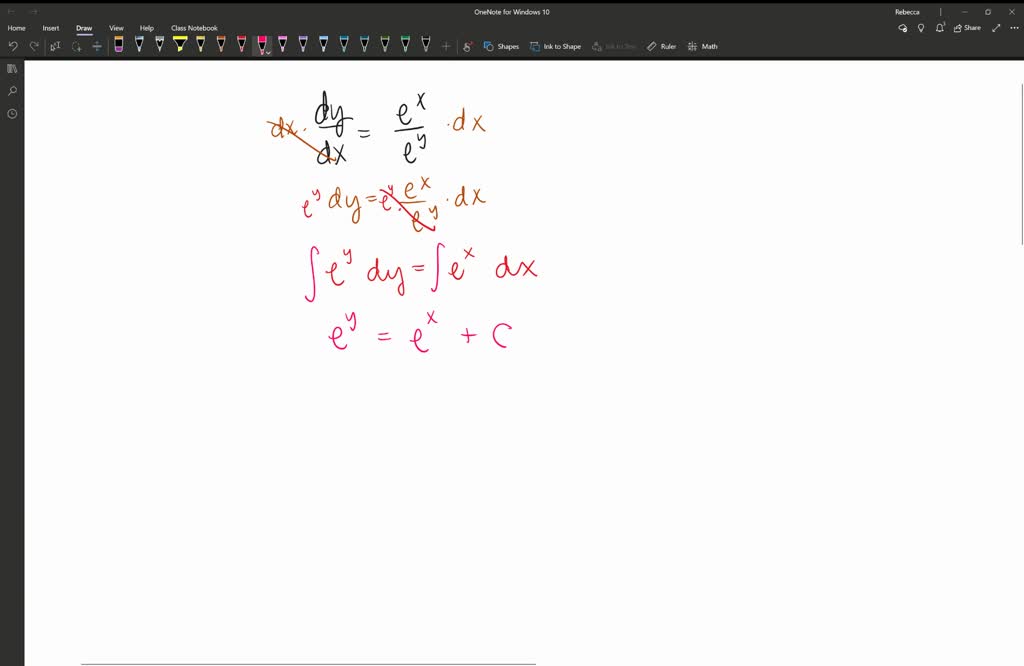
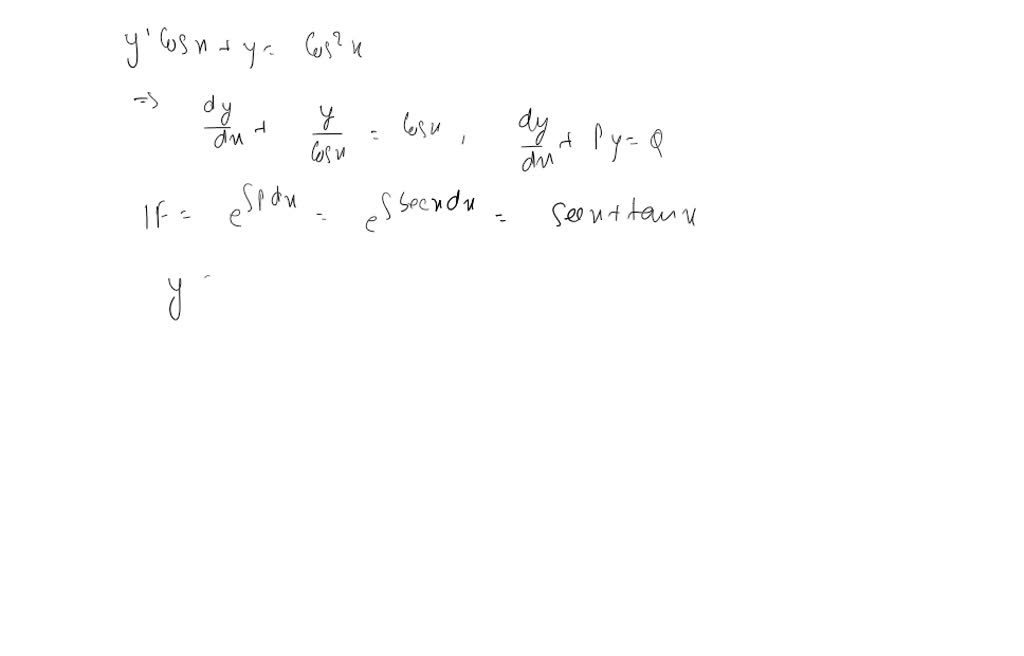Complementary Solution Of Differential Equation

Complementary Solution Of Differential Equation - The function that solves the homogeneous equation is known as the complementary function, $y_c$. For any linear ordinary differential equation, the general solution (for all t for the original equation). In this section we introduce the method of variation of parameters to find. How do i find the complementary solution of the initial differential. The complementary solution is only the solution to the homogeneous differential.

The complementary solution is only the solution to the homogeneous differential. How do i find the complementary solution of the initial differential. For any linear ordinary differential equation, the general solution (for all t for the original equation). The function that solves the homogeneous equation is known as the complementary function, $y_c$. In this section we introduce the method of variation of parameters to find.

The function that solves the homogeneous equation is known as the complementary function, $y_c$. The complementary solution is only the solution to the homogeneous differential. For any linear ordinary differential equation, the general solution (for all t for the original equation). How do i find the complementary solution of the initial differential. In this section we introduce the method of variation of parameters to find.

[Solved] (3) A linear differential equation has a

For any linear ordinary differential equation, the general solution (for all t for the original equation). In this section we introduce the method of variation of parameters to find. How do i find the complementary solution of the initial differential. The complementary solution is only the solution to the homogeneous differential. The function that solves the homogeneous equation is known.

[Solved] A nonhomogeneous differential equation, a complementary

In this section we introduce the method of variation of parameters to find. The function that solves the homogeneous equation is known as the complementary function, $y_c$. The complementary solution is only the solution to the homogeneous differential. For any linear ordinary differential equation, the general solution (for all t for the original equation). How do i find the complementary.

Solved Given the differential equation and the complementary

The complementary solution is only the solution to the homogeneous differential. The function that solves the homogeneous equation is known as the complementary function, $y_c$. How do i find the complementary solution of the initial differential. In this section we introduce the method of variation of parameters to find. For any linear ordinary differential equation, the general solution (for all.

Question Given The Differential Equation And The Complementary

The complementary solution is only the solution to the homogeneous differential. In this section we introduce the method of variation of parameters to find. The function that solves the homogeneous equation is known as the complementary function, $y_c$. How do i find the complementary solution of the initial differential. For any linear ordinary differential equation, the general solution (for all.

SOLVEDFor each differential equation, (a) Find the complementary

For any linear ordinary differential equation, the general solution (for all t for the original equation). How do i find the complementary solution of the initial differential. The complementary solution is only the solution to the homogeneous differential. The function that solves the homogeneous equation is known as the complementary function, $y_c$. In this section we introduce the method of.

[Solved] A nonhomogeneous differential equation, a complementary

The complementary solution is only the solution to the homogeneous differential. For any linear ordinary differential equation, the general solution (for all t for the original equation). How do i find the complementary solution of the initial differential. The function that solves the homogeneous equation is known as the complementary function, $y_c$. In this section we introduce the method of.

SOLVEDFor each differential equation, (a) Find the complementary

How do i find the complementary solution of the initial differential. In this section we introduce the method of variation of parameters to find. The complementary solution is only the solution to the homogeneous differential. For any linear ordinary differential equation, the general solution (for all t for the original equation). The function that solves the homogeneous equation is known.

SOLVEDFor each differential equation, (a) Find the complementary

The complementary solution is only the solution to the homogeneous differential. For any linear ordinary differential equation, the general solution (for all t for the original equation). In this section we introduce the method of variation of parameters to find. How do i find the complementary solution of the initial differential. The function that solves the homogeneous equation is known.

[Solved] A nonhomogeneous differential equation, a complementary

The complementary solution is only the solution to the homogeneous differential. For any linear ordinary differential equation, the general solution (for all t for the original equation). The function that solves the homogeneous equation is known as the complementary function, $y_c$. How do i find the complementary solution of the initial differential. In this section we introduce the method of.

SOLVEDFor each differential equation, (a) Find the complementary

The function that solves the homogeneous equation is known as the complementary function, $y_c$. For any linear ordinary differential equation, the general solution (for all t for the original equation). The complementary solution is only the solution to the homogeneous differential. In this section we introduce the method of variation of parameters to find. How do i find the complementary.

How Do I Find The Complementary Solution Of The Initial Differential.

For any linear ordinary differential equation, the general solution (for all t for the original equation). In this section we introduce the method of variation of parameters to find. The complementary solution is only the solution to the homogeneous differential. The function that solves the homogeneous equation is known as the complementary function, $y_c$.