Are All Absolute Value Functions Differentiable

Are All Absolute Value Functions Differentiable - Note that the tangent line. Let u be a differentiable real. Let |x| be the absolute value of x for real x. The function jumps at $x$, (is not continuous) like what happens at a step on a flight of stairs. \mathbb{r} \rightarrow \mathbb{r}$ we wish to. Given a differentiable function $f: Looking at different values of the absolute value function in some plots:

The function jumps at $x$, (is not continuous) like what happens at a step on a flight of stairs. Looking at different values of the absolute value function in some plots: \mathbb{r} \rightarrow \mathbb{r}$ we wish to. Let u be a differentiable real. Let |x| be the absolute value of x for real x. Given a differentiable function $f: Note that the tangent line.

Let |x| be the absolute value of x for real x. \mathbb{r} \rightarrow \mathbb{r}$ we wish to. The function jumps at $x$, (is not continuous) like what happens at a step on a flight of stairs. Given a differentiable function $f: Let u be a differentiable real. Looking at different values of the absolute value function in some plots: Note that the tangent line.

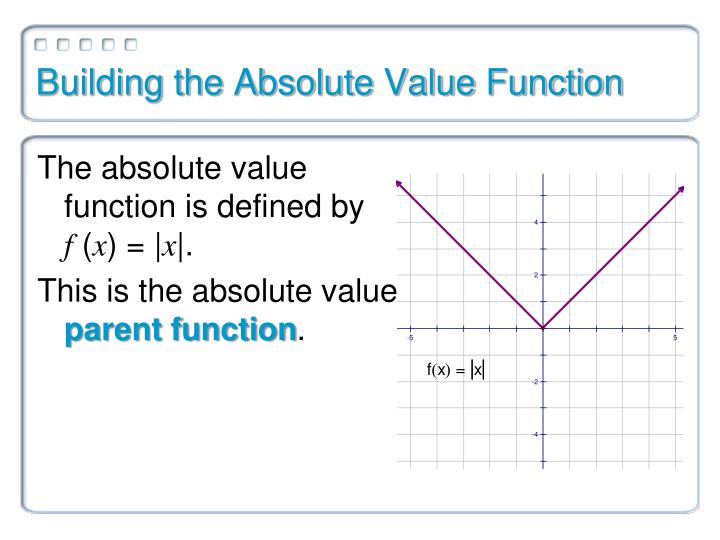
Absolute Value Functions Transformations Investigation Light Bulb

The function jumps at $x$, (is not continuous) like what happens at a step on a flight of stairs. Looking at different values of the absolute value function in some plots: Given a differentiable function $f: Let |x| be the absolute value of x for real x. Note that the tangent line.

[Solved] The differentiable functions ( f ) and ( g )

The function jumps at $x$, (is not continuous) like what happens at a step on a flight of stairs. Note that the tangent line. Let u be a differentiable real. \mathbb{r} \rightarrow \mathbb{r}$ we wish to. Given a differentiable function $f:

SOLUTION Absolute value functions Studypool

\mathbb{r} \rightarrow \mathbb{r}$ we wish to. Given a differentiable function $f: Let u be a differentiable real. Let |x| be the absolute value of x for real x. Looking at different values of the absolute value function in some plots:

calculus Differentiable approximation of the absolute value function

Let |x| be the absolute value of x for real x. \mathbb{r} \rightarrow \mathbb{r}$ we wish to. Note that the tangent line. The function jumps at $x$, (is not continuous) like what happens at a step on a flight of stairs. Given a differentiable function $f:

PPT 2.7 Absolute Value Functions and Graphs PowerPoint Presentation

Given a differentiable function $f: The function jumps at $x$, (is not continuous) like what happens at a step on a flight of stairs. Let |x| be the absolute value of x for real x. Looking at different values of the absolute value function in some plots: Let u be a differentiable real.

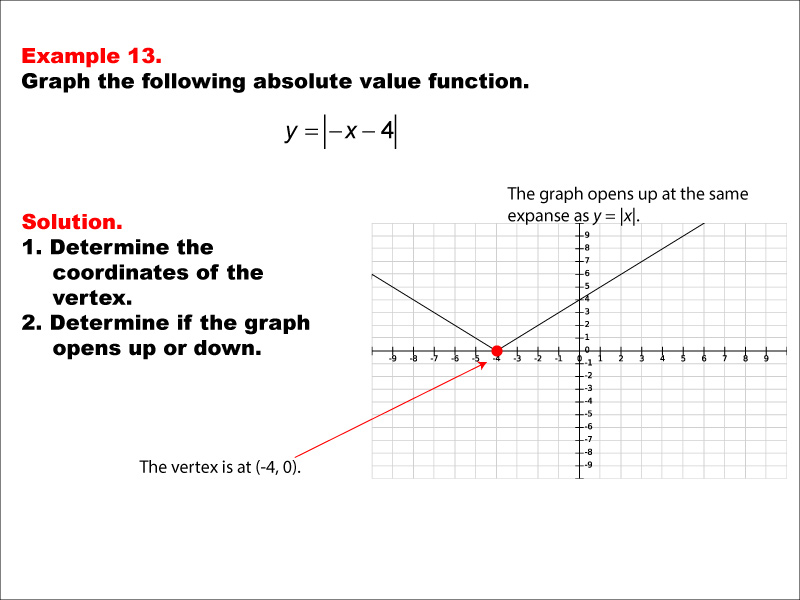
Math Example Absolute Value Functions Example 13 Media4Math

The function jumps at $x$, (is not continuous) like what happens at a step on a flight of stairs. Given a differentiable function $f: Let |x| be the absolute value of x for real x. \mathbb{r} \rightarrow \mathbb{r}$ we wish to. Let u be a differentiable real.

Absolute value functions PPT

Looking at different values of the absolute value function in some plots: Given a differentiable function $f: \mathbb{r} \rightarrow \mathbb{r}$ we wish to. Let u be a differentiable real. Let |x| be the absolute value of x for real x.

calculus How do I prove if the following functions are differentiable

Let u be a differentiable real. \mathbb{r} \rightarrow \mathbb{r}$ we wish to. Note that the tangent line. Given a differentiable function $f: Looking at different values of the absolute value function in some plots:

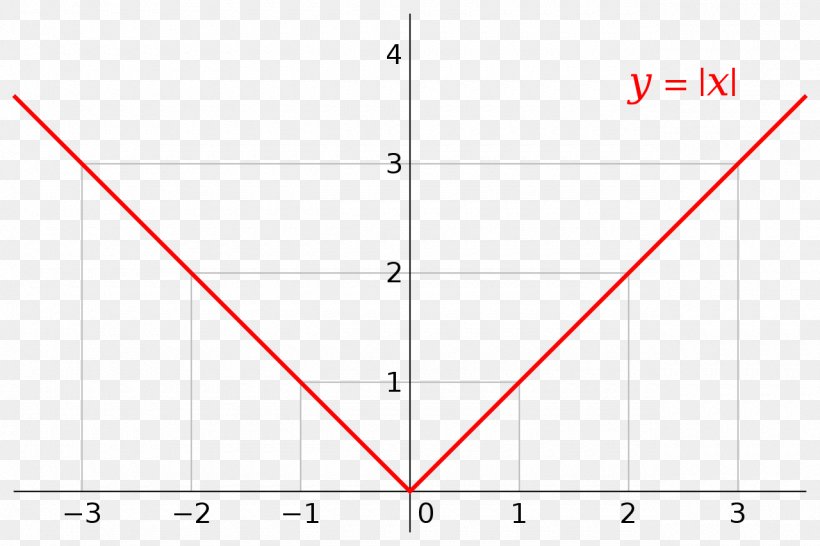
Absolute Value Graph Of A Function Differentiable Function Real Number

Looking at different values of the absolute value function in some plots: Let u be a differentiable real. Note that the tangent line. Given a differentiable function $f: Let |x| be the absolute value of x for real x.

Why is the absolute value function not differentiable at 0 Quizlet

\mathbb{r} \rightarrow \mathbb{r}$ we wish to. Let u be a differentiable real. Looking at different values of the absolute value function in some plots: Let |x| be the absolute value of x for real x. Given a differentiable function $f:

Let |X| Be The Absolute Value Of X For Real X.

Looking at different values of the absolute value function in some plots: Let u be a differentiable real. Note that the tangent line. \mathbb{r} \rightarrow \mathbb{r}$ we wish to.