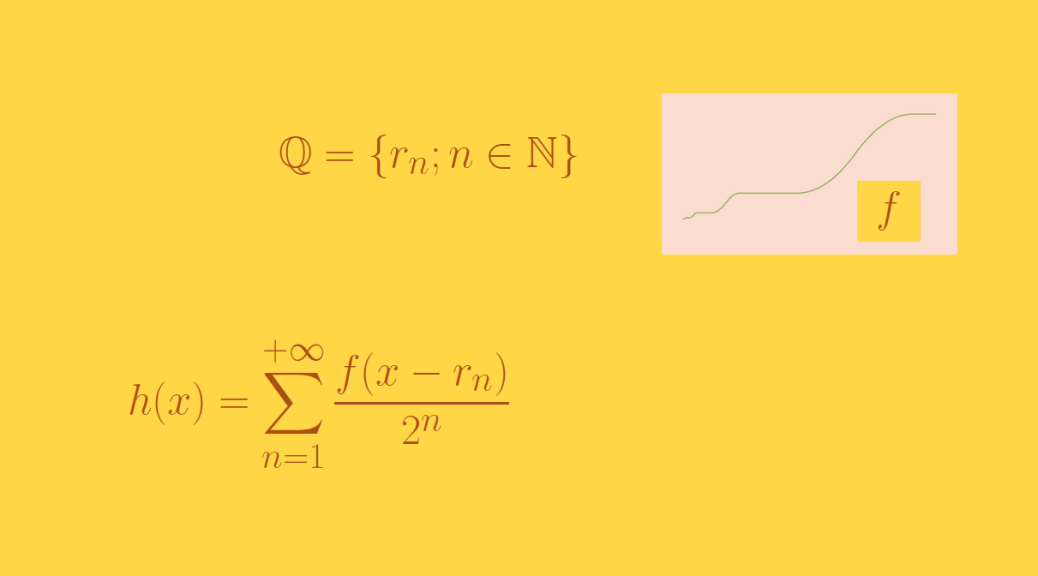Req. For Something To Be Differentiable - We'll learn how to check if a function is. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. Let's have another look at our first example: For what values of $a$ and $b$ will $f(x)$ be differentiable? To solve this question, i would like to propose the following theorem:. In this article, we'll explore what it means for a function to be differentiable in simple terms.
For what values of $a$ and $b$ will $f(x)$ be differentiable? Let's have another look at our first example: In this article, we'll explore what it means for a function to be differentiable in simple terms. To solve this question, i would like to propose the following theorem:. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. We'll learn how to check if a function is.
For what values of $a$ and $b$ will $f(x)$ be differentiable? To solve this question, i would like to propose the following theorem:. We'll learn how to check if a function is. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. Let's have another look at our first example: In this article, we'll explore what it means for a function to be differentiable in simple terms.
Can Something Be Differentiable but Not Continuous Quant RL
We'll learn how to check if a function is. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. To solve this question, i would like to propose the following theorem:. For what values of $a$ and $b$ will $f(x)$ be differentiable? Let's have another look at our first example:
Can Something Be Differentiable but Not Continuous Quant RL
To solve this question, i would like to propose the following theorem:. For what values of $a$ and $b$ will $f(x)$ be differentiable? In this article, we'll explore what it means for a function to be differentiable in simple terms. We'll learn how to check if a function is. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x.
Applicability limitations of differentiable fullreference image
For what values of $a$ and $b$ will $f(x)$ be differentiable? In this article, we'll explore what it means for a function to be differentiable in simple terms. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. Let's have another look at our first example: We'll learn how to check if a function.
Can Something Be Differentiable but Not Continuous Quant RL
Let's have another look at our first example: In this article, we'll explore what it means for a function to be differentiable in simple terms. To solve this question, i would like to propose the following theorem:. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. For what values of $a$ and $b$.
PreReq Professional Unity Developer GameDevHQ Schools
To solve this question, i would like to propose the following theorem:. Let's have another look at our first example: In this article, we'll explore what it means for a function to be differentiable in simple terms. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. We'll learn how to check if a.
A continuous function not differentiable at the rationals but
Let's have another look at our first example: To solve this question, i would like to propose the following theorem:. In this article, we'll explore what it means for a function to be differentiable in simple terms. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. We'll learn how to check if a.
Differentiable Programming A Simple Introduction
In this article, we'll explore what it means for a function to be differentiable in simple terms. Let's have another look at our first example: To solve this question, i would like to propose the following theorem:. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. For what values of $a$ and $b$.
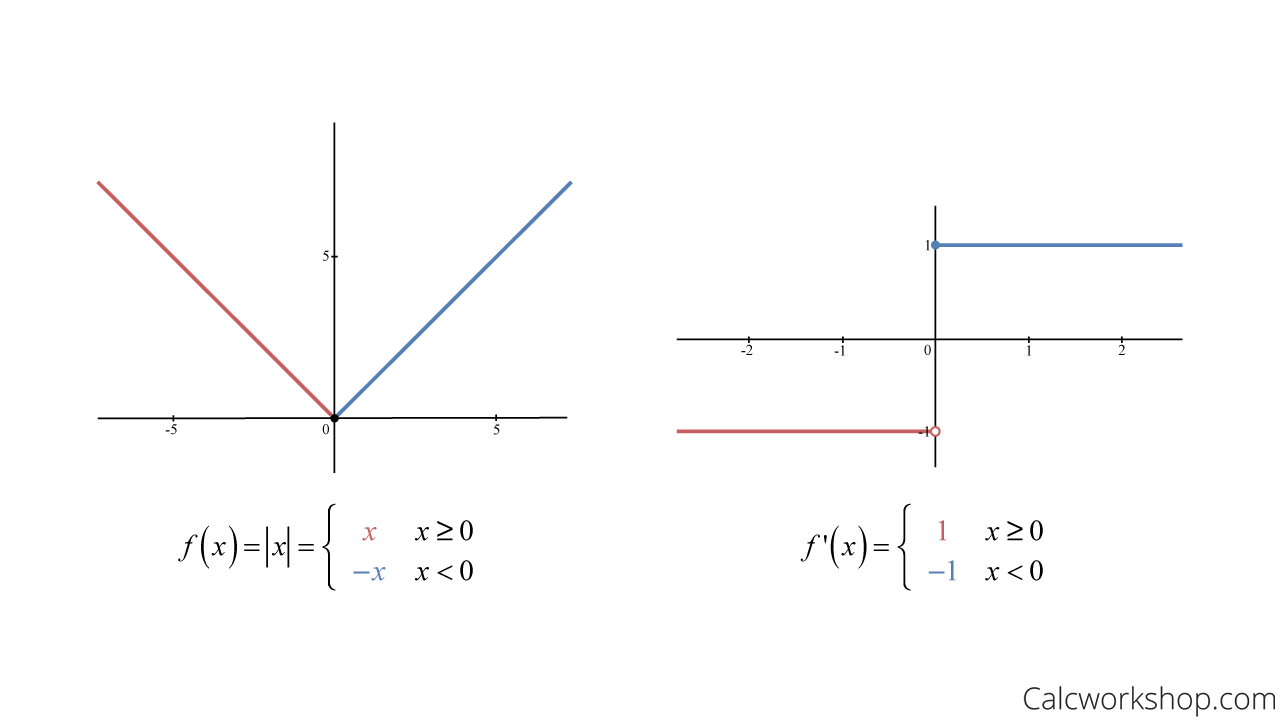
Is F(X) = X Differentiable? Exploring The Derivative Of A Simple Function
We'll learn how to check if a function is. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. For what values of $a$ and $b$ will $f(x)$ be differentiable? In this article, we'll explore what it means for a function to be differentiable in simple terms. Let's have another look at our first.
Differentiable Font download free
\mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. To solve this question, i would like to propose the following theorem:. We'll learn how to check if a function is. For what values of $a$ and $b$ will $f(x)$ be differentiable? Let's have another look at our first example:
Is F(X) = X Differentiable? Exploring The Derivative Of A Simple Function
In this article, we'll explore what it means for a function to be differentiable in simple terms. For what values of $a$ and $b$ will $f(x)$ be differentiable? Let's have another look at our first example: We'll learn how to check if a function is. To solve this question, i would like to propose the following theorem:.
To Solve This Question, I Would Like To Propose The Following Theorem:.
In this article, we'll explore what it means for a function to be differentiable in simple terms. \mathbb{r}^n \rightarrow \mathbb{r}^m [/itex] is differentiable at a point [itex] x [/itex] if all the partial. For what values of $a$ and $b$ will $f(x)$ be differentiable? Let's have another look at our first example: